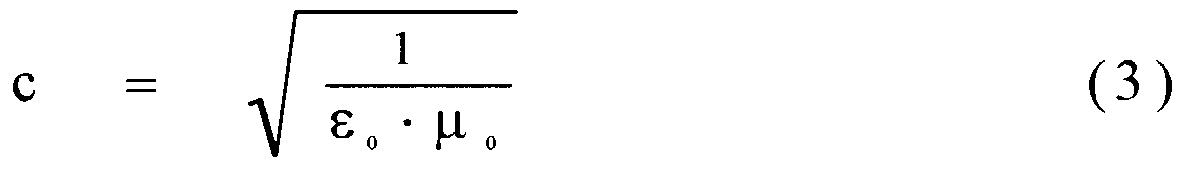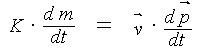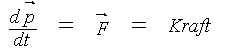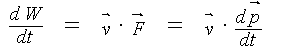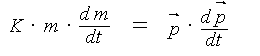Blog Ekkehard Friebe

FRIEBE, Ekkehard (1999): „Eine Alternative zur Lösung des Gravitationsproblems“ –
Die Gleichheit der trägen und schweren Masse“
Vortrag auf der DPG-Didaktik-Frühjahrstagung, Pädagogische Hochschule Ludwigsburg, am 10. März 1999

---

Zusammenfassung

Schon Albert Einstein erkannte, daß die zu seiner Zeit übliche Interpretation von NEWTONs Gravitationsgesetz mittels absolutem Raum und Fernkräften zu Widersprüchen führte. Deshalb betrachtete er im Rahmen seiner allgemeinen Relativitätstheorie das Schwerefeld nicht als ein statisches sondern als ein dynamisches Phänomen und kam dadurch zu seinem „Prinzip der Gleichheit (Äquivalenz) der trägen und schweren Masse“ (Gedankenexperiment mit dem Lift). In vorliegender Untersuchung wird dieser Gedanke weitergebildet. Es wird gezeigt, daß nicht nur der Begriff des „absoluten Raumes“ entbehrlich ist sondern daß auch die Annahme von „Fernkräften“ oder eines „kosmischen Mediums“ oder eines „gekrümmten Raumes“ entfallen kann. Diese Lösung des Gravitationsproblems ergibt sich dadurch, daß man die Eigenrotation der Himmelskörper berücksichtigt, die sowohl von NEWTON als auch von EINSTEIN vernachlässigt wurde. Berücksichtigt man nämlich diese Eigenrotation, so ergibt sich die krummlinige Bewegungsbahn der Himmelskörper ganz von selbst.

EINSTEINs Gedankenexperiment

In seinem Buch von 1917: „Über die spezielle und die allgemeine Relativitätstheorie – (Gemeinverständlich)“ schreibt ALBERT EINSTEIN im § 20 unter der Überschrift:

„Die Gleichheit der trägen und schweren Masse als Argument für das allgemeine Relativitätspostulat.“ (Zitat von S. 45/46):

„Wir denken uns ein geräumiges Stück leeren Weltraumes, so weit weg von Sternen und erheblichen Massen, daß wir mit hinreichender Genauigkeit den Fall vor uns haben, der im Galileischen Grundgesetz vorgesehen ist. Es ist dann möglich, für diesen Teil der Welt einen Galileischen Bezugskörper zu wählen, relativ zu welchem ruhende Punkte ruhend bleiben, bewegte dauernd in geradlinig gleichförmiger Bewegung verharren. Als Bezugskörper denken wir uns einen geräumigen Kasten von der Gestalt eines Zimmers; darin befinde sich ein mit Apparaten ausgestatteter Beobachter. Für diesen gibt es natürlich keine Schwere. Er muß sich mit Schnüren am Boden befestigen, wenn er nicht beim leisesten Stoß gegen den Boden langsam gegen die Decke des Zimmers entschweben will.

In der Mitte der Kastendecke sei außen ein Haken mit Seil befestigt und an diesem fange nun ein Wesen von uns gleichgültiger Art mit konstanter Kraft zu ziehen an. Dann beginnt der Kasten samt dem Beobachter in gleichförmig beschleunigten Fluge nach „oben“ zu fliegen. Seine Geschwindigkeit wird im Laufe der Zeit ins Phantastische zunehmen – falls wir all dies beurteilen von einem anderen Bezugskörper aus, an dem nicht mit einem Stricke gezogen wird.

Wie beurteilt aber der Mann im Kasten den Vorgang? Die Beschleunigung des Kastens wird vom Boden desselben durch Gegendruck auf ihn übertragen. Er muß also diesen Druck mittels seiner Beine aufnehmen, wenn er nicht der ganzen Länge nach den Boden berühren will. Er steht dann im Kasten genau wie einer in einem Zimmer eines Hauses auf unserer Erde steht. Läßt er einen Körper los, den er vorher in der Hand hatte, so wird auf diesen die Beschleunigung des Kastens nicht mehr übertragen; der Körper wird sich daher in beschleunigter Relativbewegung dem Boden des Kastens nähern. Der Beobachter wird sich ferner überzeugen, daß die Beschleunigung des Körpers gegen den Boden immer gleich groß ist, mit was für einem Körper er auch den Versuch ausführen mag.

BILD 1: Massen-Äquivalenz

Der Mann im Kasten wird also, gestützt auf seine Kenntnisse vom Schwerefelde, wie wir sie im letzten Paragraphen besprochen, zu dem Ergebnis kommen, daß er samt dem Kasten sich in einem ziemlich konstanten Schwerefeld befinde. Er wird allerdings einen Augenblick verwundert sein darüber, daß der Kasten in diesem Schwerefeld nicht falle. Da entdeckt er aber den Haken in der Mitte der Decke und das an demselben gespannte Seil, und er kommt folgerichtig zu dem Ergebnis, daß der Kasten in dem Schwerefeld ruhend aufgehängt sei.

Dürfen wir über den Mann lächeln und sagen, er befinde sich mit seiner Auffassung im Irrtum? Ich glaube, wir dürfen das nicht, wenn wir konsequent bleiben wollen, sondern wir müssen zugeben, daß seine Auffassungsweise weder gegen die Vernunft noch gegen die bekannten mechanischen Gesetze verstößt. Wir können den Kasten, wenn er auch gegen den zuerst betrachteten „Galileischen Raum“ beschleunigt ist, dennoch als ruhend ansehen. Wir haben also guten Grund, das Relativitätsprinzip auszudehnen auf relativ zueinander beschleunigte Bezugskörper und haben so ein kräftiges Argument für ein verallgemeinertes Relativitätspostulat gewonnen.<<

Bei diesem Gedankenexperiment EINSTEINs, das durch BILD 1 veranschaulicht wird (Bild 1 selbst stammt nicht von Einstein), wird das Schwerefeld nicht als ein statisches sondern als ein dynamisches Phänomen betrachtet.

Berücksichtigung von Rotationen

Das Gedankenexperiment enthält jedoch ein wesentliches Problem:
Da eine konstante Hubkraft vorausgesetzt ist, beginnt (mit Einsteins eigenen Worten) der Kasten samt dem Beobachter in gleichförmig beschleunigtem Fluge nach „oben“ zu fliegen. Seine Geschwindigkeit wird im Laufe der Zeit ins Phantastische zunehmen.

Eine Geschwindigkeit oberhalb der Lichtgeschwindigkeit ist aber laut Lehrbuchaussagen unmöglich. Außerdem widerspricht sie der speziellen Relativitätstheorie, die von EINSTEIN selbst stammt. Das Gedankenexperiment führt sich also scheinbar selbst ad absurdum.

Ganz anders wird jedoch die Interpretation, wenn man berücksichtigt, daß praktisch alles im Kosmos rotiert. Bei Rotationen können nämlich ständig gleichbleibende Beschleunigungen und damit Beschleunigungskräfte aufrecht erhalten werden, ohne daß irgend eine Größe phantastische Werte erreicht oder überschreitet. Dies ist jedem Physiker durch die Zentrifugalbeschleunigung und die Zentrifugalkraft geläufig.

Wie läßt sich diese Analogie auf das Gedankenexperiment EINSTEINs übertragen?

Das 1. Axiom NEWTONs vernachlässigt die Rotation der Himmelskörper, wie an anderer Stelle (FRIEBE 1998) bereits gezeigt wurde. Dort wurde auch begründet, warum dieses Axiom folgender Neufassung bedarf:

Jeder Körper ohne Drehimpuls beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.

Durch den Zusatz „ohne Drehimpuls“ wird eine mehr als 300 Jahre alte, dogmatische Einschränkung aufgehoben und der Weg frei, das Bewegungsverhalten von Körpern mit Drehimpuls zutreffend zu beschreiben. Es folgt nämlich, daß sich bewegte Körper „mit Drehimpuls“ auf krummlinigen Bahnen, vorzugsweise Kreisen, bewegen. Dabei ist die Bahnkrümmung eine Funktion des Verhältnisses Impuls / Drehimpuls, die Orientierung der krummlinigen Bahn eine Funktion der vektoriellen Richtung des Drehimpulses.

Das klassische Gesetz für Zentrifugalkräfte und Zentrifugalbeschleunigungen bedarf in diesem Zusammenhang einer Abänderung. Die vom Verhältnis Impuls / Drehimpuls bestimmte kreisförmige Bahn stellt eine Grenzkurve dar. Bei Vergrößerung des Verhältnisses wird der bewegte Körper – von der Grenzkurve ausgehend – nach außen zu einer Kreisbahn mit größerem Radius wegfliegen, bei Verkleinerung dagegen wird er nach innen zu einer Kreisbahn mit kleinerem Radius streben. Ein Himmelskörper, bei dem das Verhältnis Impuls / Drehimpuls über sehr lange Zeit konstant bleibt, bewegt sich daher auf einer fest vorgegebenen, vorzugsweise kreisförmigen Bahn. Die krummlinige Bewegungsbahn der Himmelskörper ergibt sich also ganz von selbst aufgrund ihrer Eigenrotation, die sowohl von NEWTON als auch von EINSTEIN vernachlässigt wurde.

Geht man beim Gedankenexperiment Einsteins statt von einer linearen Beschleunigung nun von einer kreisförmigen Beschleunigung aus, wie sie auf der Erdoberfläche wegen der Erdrotation ohnehin gegeben ist, wobei diese Beschleunigung im klassischen Sinne eine senkrecht von der Erdoberfläche weggerichtete Zentrifugalbeschleunigung ist (BILD 2), so ergibt sich folgendes:

BILD 2: Klassische Auffassung der Zentrifugalbeschleunigung

Aufgrund der vorstehenden Überlegungen bezüglich einer Grenzkurve gibt es einen Bereich, bei dem ein Streben nach innen vorliegt. Man könnte von einer negativen Zentrifugalbeschleunigung sprechen. Und diese empfinden wir als Schwerebeschleunigung (Schwerkraft).

Vorstehende Gedanken sollen noch etwas deutlicher gemacht werden: Die klassische Aussage der Zentrifugalbeschleunigung senkrecht zur Erdoberfläche bezieht sich ausschließlich auf den mitdrehenden Beobachter. Losgelöst hiervon betrachtet liegt ein Bestreben vor, die Bewegung eines Massekörpers aufgrund seiner Massenträgheit in einer tangential verlaufenden, geradlinigen Bahn verharren zu lassen. Nach der neuen Interpretation liegt demgegenüber ein Bestreben vor, die Bewegung eines Massekörpers in der gekrümmten Grenzkurve verharren zu lassen. Würde sich ein Massekörper von der Erdoberfläche lösen, so würde seine Bewegungsbahn längs der gekrümmten Grenzkurve verlaufen. Hierbei muß allerdings vorausgesetzt werden, daß kein Hindernis dem entgegensteht, beispielsweise die weniger stark gekrümmte Erdoberfläche. In diesem Fall entsteht ein Zwangszustand, den wir als negative Zentrifugalbeschleunigung und damit – wie gesagt – als Schwerebeschleunigung (Schwerkraft) empfinden. Die Annahme einer Massen-Anziehungskraft (Fernkraft) ist nicht mehr erforderlich. Ebenso kann die Annahme eines absoluten Raumes, eines kosmischen Mediums oder eines gekrümmten Raumes entfallen.

Es könnte jetzt der Einwand erhoben werden, daß die von NEWTON postulierte Massen-Anziehungskraft durch zahlreiche Experimente bestätigt worden sei. Diese Aussage bedarf einer Klarstellung.

Viele Wissenschaftler glauben, die von den Experimentalphysikern vorgelegten Meßergebnisse seien unverrückbare Tatsachen. Dies ist nicht der Fall. Denn fast alle modernen Meßverfahren sind theoriegeleitete Meßverfahren, die zusätzlich einer mathematisch-rechnerischen Auswertung bedürfen. Das heißt: Es besteht ein echtes Wechselspiel zwischen Theorie und Experiment derart, daß ein und dasselbe Experiment zwei oder mehr als zwei Interpretationen zuläßt, je nachdem, von welcher Hintergrundüberzeugung (Paradigma) man ausgeht. Dabei können sich diese Interpretationen ganz wesentlich voneinander unterscheiden. Dieser Sachverhalt ist besonders klar dargelegt in der Arbeit KUHN, W. (1983): „Das Wechselspiel von Theorie und Experiment im physikalischen Erkenntnisprozeß“. Das aufmerksame Studium dieser Arbeit wird empfohlen.

Der Glaube an die Weltmaschine

In gleicher Richtung zielen auch die Ausführungen von TETENS (1984). „Der Glaube an die Weltmaschine. – Zur Aktualität der Kritik Hugo Dinglers am physikalischen Weltbild“. Hierin wird u. a. ausgesagt (Zitate von Seite 95/96):

>>Nun gehen Störungen gerade von solchen natürlichen Bedingungen und Vorgängen aus, die wir noch nicht „in unsere Apparate eingefangen und isoliert“ (Dingler) haben. Physiker suchen in einem solchen Fall nach einem Wissen darüber, wie man Störungen ausschalten und beseitigen kann. So haben etwa farbige Ränder an Linsen, die die Beobachtungen mit optischen Geräten beeinträchtigen, den Anstoß gegeben zu Fragestellungen, die auf wichtige theoretische „Gesetze“ der Optik führten, oder wurden die Hauptsätze der Thermodynamik aufgestellt im Zusammenhang mit Bemühungen, Prozesse zu koppeln und den Wirkungsgrad dabei zu optimieren. Jedenfalls bedienen sich die Physiker bei dem Versuch, Störungsbeseitigungswissen zu entwickeln, wieder der experimentellen Methode, so daß zugleich mit Gesetzen für solche Störungen auch Apparate oder verbesserte Versionen der ursprünglichen Apparate zur Hand sind, die diese Gesetze funktional erfüllen. . . . . . . . . Da wir Natur nicht einfach im Labor imitieren, tragen die sogenannten Naturgesetze ihren Namen ganz zu Unrecht. Würden wir sie, was methologisch viel gerechtfertigter wäre, Apparategesetze nennen, würde bei uns viel eher das Bewußtsein dafür wachgehalten, daß unsere „natur“wissenschaftlichen Laborresultate in einem tendenziellen Widerstreit zur Natur „draußen“ stehen.<<

Unter Berücksichtigung dieser Gedanken ergibt sich, daß alle sogenannten experimentellen Bestätigungen von NEWTONs Gravitationsgesetz – wegen unzulässiger Extrapolationen der Meßwerte – unschlüssig sind.
(siehe auch: FAHR / KNAPP 1989)

Literatur

DINGLER, H. (1987): „Aufsätze zur Methodik“, herausgegeben von Ulrich Weiß, Felix Meiner Verlag, Hamburg

DUHEM, P. (1908): „Ziel und Struktur der physikalischen Theorie“, Leipzig 1908 und Hamburg 1976

EINSTEIN, A. (1917): „Über die spezielle und die allgemeine Relativitätstheorie (Gemeinverständlich)“, Verlag Friedr. Vieweg, Braunschweig

FAHR, H.-J. / KNAPP, W. (1989): „Newtons Gravitationsgesetz . . . nur die halbe Wahrheit?“ aus Zeitschr. „bild der wissenschaft“, H. 3/89, S. 49 – 58

FRIEBE, E. (1998): „Das 1. Axiom NEWTONs – Ursache der weltweiten Krise der Physik“, DPG- Didaktik Frühjahrstagung, Regensburg.

HERMAN, R. (1991): „FUSION – The search for endless energy“, Cambridge University Press, Cambridge, New York, Port Chester, Melbourne, Sydney

KUHN, W. (1983): „Das Wechselspiel von Theorie und Experiment im physikalischen Erkenntnisprozeß“, DPG-Didaktik-Tagungsband 1983, S. 416 – 438

TETENS, H. (1984): „Der Glaube an die Weltmaschine – Zur Aktualität der Kritik Hugo Dinglers am physikalischen Weltbild“, aus: Janich, P. (Hrsg.): „Methodische Philosophie – Beiträge zum Begründungsproblem der exakten Wissenschaften in Auseinandersetzung mit Hugo Dingler“, Bibliographisches Institut Mannheim, Wien, Zürich

THÜRING, B. (1967): „Die Gravitation und die philosophischen Grundlagen der Physik“, Verlag Duncker & Humblot, Berlin

WALKER, J. (1990): „Ein Ball mit Drall“, Fischer Taschenbuch Verlag GmbH, Frankfurt am Main

---

• Homepage

FRIEBE, Ekkard (1997): „Die mathematischen Irrtümer von Isaac NEWTON“,
Vortrag auf der DPG-Didaktik-Frühjahrstagung am 12. März 1997 in Berlin.

a) Zusammenfassung

Isaac NEWTON gilt allgemein als hervorragender Mathematiker. Es überrascht deshalb, daß Albrecht FÖLSING in seinem Buch von 1984: „Der Mogelfaktor“ auf Seite 91 schreibt (Zitat): „Eine peinlich genaue Analyse von NEWTONs Rechnungen, die der amerikanische Wissenschaftshistoriker Richard S. WESTFALL im Jahre 1973 veröffentlicht hat, förderte zutage, daß NEWTON sich die erstrebte Genauigkeit durch eine Vielzahl gekonnter kleiner Korrekturen ermogelt hatte“. Die Untersuchungen von WESTFALL betreffen hauptsächlich die Anpassung der Experimente an die Theorie. Es soll in meinem Vortrag gezeigt werden, daß NEWTON bereits bei seinem Versuch, unabhängig von dem empirisch begründeten 3. KEPLERschen Gesetz die Abhängigkeit der „Centripetalkraft“ entsprechend 1/r² mathematisch nachzuweisen, grundlegende mathematische Irrtümer unterlaufen sind.

.

b) Veranlassung

In dem im Jahre 1989 erschienenen Buch: „Hegels Deutung der Gravitation – Eine Studie zu Hegel und Newton“ von Karl-Norbert IHMIG befindet sich folgende Aussage (Zitat von Seite 27 Mitte, ohne Anmerkungen):

„Schon 1645 plädierte Bullialdus in seiner Astronomia Philolaica (im Gegensatz zu Kepler, der das einfache reziproke Verhältnis favorisierte) für eine Abnahme der Sonnenkraft im quadratischen Verhältnis der Entfernung. Ein anderes Beispiel wäre R. Hooke, der in einem Brief an Newton vom 6. 1. 1680 schrieb:

„But my supposition is that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall.“

Das Problem lag für Hooke, wie für alle Newtonschen Vorgänger, darin, daß sie diese Abhängigkeit stets nur als gewisse Plausibilitätsannahmen aussprechen, aber nicht beweisen konnten. Newton gelang es, mittels der Huygensschen Formel für die Zentrifugalkraft ( F = n · v²/r ) und dem 3. Keplerschen Gesetz das „inverse-square-law“ zunächst für Kreise mathematisch abzuleiten. Im dritten Abschnitt des ersten Buches der Principia beweist Newton die Gültigkeit dieses Gesetzes, und darin ist wohl seine eigentliche mathematische Leistung zu sehen, auch für Ellipsen (sowie für andere Kegelschnitte). Mit der Bewunderung für die mathematische Genialität Newtons trat für viele die physikalische Bedeutung seines Werkes immer mehr in den Hintergrund; ein Effekt, der sicherlich von Newton selbst nicht ganz unbeabsichtigt war und der natürlich die Reibungspunkte mit Cartesianern erheblich verminderte.“

Dieser Hinweis zusammen mit den kritischen Äußerungen von FÖLSING (siehe Zusammenfassung oben) war für uns Veranlassung, die genannte mathematische Ableitung im dritten Abschnitt des ersten Buches der Principia einer kritischen Überprüfung zu unterziehen.

.

c) Die mathematische Begründung der Abhängigkeit nach 1/r²

Es folgt nachstehend eine auszugsweise Wiedergabe des § 29 des dritten Abschnittes des ersten Buches von Newton, deutschsprachige Fassung, herausgegeben von Prof. Dr. J. Ph. WOLFERS, Berlin 1872 (Zitat):

Abschnitt III.

Von der Bewegung der Körper in excentrischen Kegelschnitten

§. 29. Aufgabe. Ein Körper bewegt sich in einer Ellipse; man sucht das Gesetz der nach ihrem Brennpunkt gerichteten Centripetalkraft. Es sei S der Brennpunkt der Ellipse. Man ziehe SP, welche den Durchmesser DK in E und die Ordinate Qv in x schneidet und vollende das Parallelogramm QxPR.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Zweiter Beweis. Da die nach dem Mittelpunkte der Ellipse gerichtete Kraft, vermöge welcher der Körper P sich auf jener bewegen kann, (nach §. 27., Zusatz 1.) dem Abstande PC des Körpers vom Mittelpunkte proportional ist; so ziehe man CE der Tangente PR parallel. Alsdann wird die Kraft, vermöge welcher derselbe Körper P sich um irgend einen anderen Punkt S in der Ellipse bewegen kann, wenn CE und PS sich in E schneiden, (nach §. 22., Zusatz 3.)

(PE³) / (PS²) ,

d. h. wenn S der Brennpunkt der Ellipse, also PE constant ist, indirekt

PS²

proportional. (Ende des Zitats)

Vorstehend ist nur der zweite Beweis des § 29 wiedergegeben, da dieser wesentlich kürzer ist als der erste Beweis und weil außerdem hierin die Unhaltbarkeit der gegebenen Ableitung besonders deutlich wird.

Durch Anwendung der black-box-Methode (ANNAHME, die eigentliche Ableitung sei in einem unzugänglichen schwarzen Kasten verborgen, die Prämissen und das Endergebnis seien aber bekannt) kann man nämlich bereits ohne Kenntnisnahme der Ableitungen der §§ 27 und 22 erkennen, daß das Endergebnis falsch sein muß.

Einerseits soll die nach dem Mittelpunkte C der Ellipse gerichtete Kraft dem Abstande PC des Körpers vom Mittelpunkte proportional sein, andererseits soll aber die nach dem Brennpunkte S gerichtete Kraft umgekehrt proportional dem Quadrat des Abstandes PS sein. Durch einen einfachen Grenzwertübergang von der Ellipse zum Kreis (der Kreis ist eine spezielle Form einer Ellipse) ist erkennbar, daß diese Aussage zu einem Widerspruch führt (Unstetigkeit des Grenzwertüberganges).

Was ist hier geschehen? Die vorausgesetzte, in § 27 gegebene Ableitung, die eine Ellipse als gegeben annimmt, ist fehlerfrei. Aus ihr folgt die am Anfang genannte Proportionalität. Zutreffend ist auch die Aussage, daß – für ein und dieselbe Ellipse – die Strecke PE konstant ist, wenn S der Brennpunkt der Ellipse ist. Fehlerhaft ist jedoch die Ableitung des § 22, die ihrerseits auf § 21 Bezug nimmt. Im § 21 wird nämlich eine Aussage, die für den Mittelpunkt C zutrifft, ohne stichhaltige Begründung auf andere Punkte, beispielsweise den Brennpunkt S, übertragen.

Die genannte Proportionalität folgt unmittelbar aus der Annahme einer Ellipse durch Newton. Und hierfür ist nur diese Proportionalität mathematisch korrekt.

Es ergibt sich daher, daß das „inverse-square-law“ (1/r²-Gesetz) für Ellipsen (und andere Kegelschnitte, z. B. Kreise) mathematisch falsch ist. Und gerade dieses sogenannte „Gesetz“ betrachtet Karl-Norbert IHMIG als NEWTONs eigentliche mathematische Leistung.

Ergänzend sei bemerkt, daß auch der erste Beweis des § 29 fehlerhaft ist, da er ebenfalls auf § 21 Bezug nimmt. Zusätzlich ist aber hierin noch ein die Infinitesimalrechnung betreffender Fehler enthalten. Eine ausführliche Analyse dieses Problems finden Sie unter: DPG-Frühjahrstagung 1997

.

d) Die empirische Begründung der Abhängigkeit nach 1/r²

Es soll nun noch die NEWTON’sche Untersuchung für Kreise kurz angesprochen werden, auf die Karl-Norbert IHMIG hinweist (Zitat oben). Diese wird im zweiten Abschnitt des ersten Buches gebracht. Dort heißt es im § 18 (Zitat):

„Zusatz 6. Sind die Quadrate der Umlaufzeiten den Cuben der Radien proportional, so verhalten sich die Centripetalkräfte indirekt wie die Quadrate der Radien, die Geschwindigkeiten aber indirekt wie die Quadratwurzeln der Radien; und umgekehrt.“

Man erkennt hierin im ersten Halbsatz der Aussage direkt das 3. KEPLER’sche Gesetz wieder, welches lautet:

Für alle Planetenbahnen ist das Verhältnis r³ / T² konstant.

Newton bringt aber für seine Aussage keine mathematische Ableitung, da er diese offenbar als bekannt voraussetzt. Er ergänzt hierzu jedoch folgende Anmerkung (Zitat aus § 19):

„Der Fall des Zusatzes 6. findet bei der Bewegung der Himmelskörper statt (wie Wren, Hook und Halley ursprünglich gefunden haben), weshalb ich dasjenige, was sich auf die Abnahme der Centripetalkräfte im doppelten Verhältnis der Radien bezieht, im Folgenden näher auseinandersetzen werde.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Durch derartige Sätze hat Huygens in seinem vortrefflichen Werke über Pendeluhren die Kraft der Schwere mit den Centrifugalkräften umlaufender Körper verglichen.“

Erst in einer Erläuterung von Professor Dr. WOLFERS in der von ihm 1872 herausgegebenen deutschen Ausgabe der „Mathematischen Prinzipien der Naturlehre“ wird die genannte Aussage Newtons mittels des 3. KEPLER’schen Gesetzes und der HUYGENS’schen Formel für die Zentrifugalkraft abgeleitet. Wolfers bezieht sich dabei auf die verbalen Aussagen in Newtons § 18, die der Huygens’schen Formel entsprechen. Unsere Überprüfung hat die Richtigkeit dieser Ableitung ergeben.

Allerdings wird bei dieser Ableitung vorausgesetzt, daß das sogenannte 1. Gesetz Newtons:

1. Gesetz  Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern (Zitat nach WOLFERS 1872, S. 32)

ein allgemeingültiges Naturgesetz sei. In Wirklichkeit handelt es sich hierbei jedoch um ein Axiom im Sinne einer Festsetzung (Definition).

Außerdem ist das 3. KEPLER’sche Gesetz ein rein empirisches Gesetz, das nur für die damals bekannten Planeten experimentell bestätigt wurde. Die Newton’sche Aussage gemäß Zusatz 6 (Abhängigkeit gemäß 1/r² ), die etwa 200 Jahre lang von der überwiegenden Mehrzahl der Naturwissenschaftler als naturgesetzlich angesehen worden war, ist daher kein Naturgesetz sondern ebenfalls nur ein Axiom.

Es ergibt sich also die bemerkenswerte Tatsache, daß dasjenige, was Newton selbst rechnete, im Rahmen der vorgegebenen Prämissen mathematisch falsch war, während dasjenige, was als das Newton’sche Gravitationsgesetz in die Lehrbücher eingegangen ist, bereits von seinen Vorgängern formuliert worden war.

.

e) Eine neue Interpretation der Schwerkraft

Bereits in dem im Jahre 1895 erschienenen Buch von ROSENBERGER: „Isaac Newton und seine physikalischen Principien“ werden wesentliche Zweifel an der Allgemeingültigkeit des sogenannten Gravitationsgesetzes laut. Wegen seiner Wichtigkeit ist dieses Buch im Jahre 1978 als Reprint neu erschienen. In der Schlußbetrachtung dieses Buches auf S. 527 heißt es beispielsweise (auszugsweises Zitat):

„Die fast göttliche Autorität, welche NEWTON’s Lehren in dem ersten Jahrhundert nach ihrem Auftreten genossen, hat sich in den letzten fünfzig Jahren stark vermindert und die Verehrung NEWTON’s ist stellenweise in das Gegenteil verkehrt worden. Statt eines genialen Reformators, eines originellen Begründers der wahren Wissenschaft hat man in ihm nur noch einen zwar sehr fleißigen, aber doch höchst mittelmäßig begabten Forscher sehen wollen, der ein gänzlich verfehltes System der Optik zur Geltung gebracht, der nur aus den KEPLER’schen Gesetzen die schon darin enthaltene Idee der Gravitation ausgezogen und für seine Erfindung ausgegeben, und der endlich eine noch ziemlich verworrene Vorstellung von der Infinitesimalrechnung gehabt habe.

Müßten wir notwendig uns für eine der extremen Meinungen entscheiden, so würden wir trotz unserer oft entgegengesetzt scheinenden Ausführungen sicher nicht die letztere wählen. Es ist immer mißlich, geistige Größen ihrem Werte nach vergleichen und ihrer Größe nach ordnen zu wollen. Trotzdem darf man doch sagen, daß, Alles in Allem betrachtet, NEWTON an geistiger Kraft und Schärfe so weit über das gewöhnliche menschliche Maß hinausgeragt hat, wie weit wir das nur je an einem gottbegnadeten Menschen erfahren haben. Wenn wir in der vorliegenden Arbeit uns bemüht haben, neben den Momenten seiner Größe auch die Unvollkommenheiten, die Fehler und die menschlichen Schwächen an NEWTON hervorzuheben, so geschah das nicht, weil wir ihn auf irgend eine Weise in seiner Bedeutung herabsetzen wollten, sondern nur darum, weil uns eine Berücksichtigung dieser menschlichen Erdenreste für das Verständnis der wissenschaftlichen Arbeiten NEWTON’s selbst und noch mehr für die Beurteilung der Entwickelung der Wissenschaften nach NEWTON notwendig erschien.“

Die Untersuchungen von ROSENBERGER wurden – wie gesagt – 1895 veröffentlicht. Es wurde u. a. dadurch offensichtlich, daß die Axiomatik Newtons zur Beschreibung der Gravitation nicht länger haltbar war. Deshalb wurde die Gravitationstheorie EINSTEINs (sogenannte Allgemeine Relativitätstheorie) mit viel Enthusiasmus aufgenommen. Heute zeichnet sich aber immer deutlicher ab (vgl. beispielsweise FAHR 1995, TREFIL 1994, WEINBERG 1995), daß auch diese Theorie unüberbrückbare Schwierigkeiten mit sich bringt.

Nachstehend wird nun eine neue Interpretation der Schwerkraft gegeben, welche diese als eine dynamische Größe, ähnlich der Zentrifugalkraft, als Folge der Rotation unseres Planeten ERDE um seine eigene Achse beschreibt. Diese Interpretation basiert auf der Arbeit FRIEBE (1996). Sie wird deshalb als zukunftsweisend angesehen, weil sie mit der Tatsache im Einklang steht, daß Gravitationskräfte – im Gegensatz zu allen anderen Kräften außer der Zentrifugalkraft – nicht abschirmbar sind.

Nach dieser Interpretation ist die Schwerkraft eine dynamische Größe, die mit der Zentrifugalkraft (Fliehkraft) eng verwandt ist. Fährt man beispielsweise auf dem Oktoberfest oder einem anderen Rummelplatz mit dem Ketten-Karussell, dann fliegen die Sitze aufgrund der Zentrifugalkraft nach außen. Entsprechendes erlebt man beim Rotor, einem hohlzylindrischen Karussell, bei dem die Leute an den innenliegenden Wänden „kleben“ bleiben, wenn die Rotationsgeschwindigkeit groß genug ist. Das gleiche Prinzip liegt auch NEWTONs Eimerversuch zugrunde, der in diesem Zusammenhang immer wieder genannt wird. In all diesen Fällen wird deutlich, daß die Zentrifugalkraft ein dynamischer Vorgang ist.

Die Erklärung ist einfach: Infolge der natürlichen Trägheit streben die bewegten Massen danach, ihren Bewegungszustand aufrecht zu erhalten. Würden die Ketten des Ketten-Karussells reißen, so würden die Personen samt ihren Sitzen nach außen fliegen. Die Lehrbücher sagen nun: Sie fliegen linear-gleichförmig nach außen. Ist das richtig? Keiner scheint das bisher überprüft zu haben! Es ist nämlich zu berücksichtigen, daß die Massen eine Rotationsfrequenz haben, die gleich ist der Rotationsfrequenz des Karussells, von dem sie abgeworfen wurden (Drehimpuls-Erhaltungssatz).

Die neue Interpretation der Schwerkraft geht nun davon aus, daß die bewegten Massen der Himmelskörper aufgrund ihres mitgeführten Drehimpulses auf einer vergleichsweise großen Kreisbahn weiterfliegen. Der Radius dieser Kreisbahn ist abhängig von dem Verhältnis Impuls zu Drehimpuls. Ist der Drehimpuls gleich NULL, so ist der Radius gleich unendlich, die Masse fliegt tatsächlich – entsprechend dem 1. Axiom Newtons – linear-gleichförmig. Dieser letztere Fall ist aber beim Ketten-Karussell und ähnlichen Situationen nicht gegeben.

Jeder Stein, jedes Lebewesen, jeder Mensch und selbst jedes Luftmolekül auf der Erdoberfläche wird aufgrund der Eigenrotation der ERDE in 24 Stunden einmal herumgewirbelt. Die Geschwindigkeit auf der Erdoberfläche ist gar nicht so gering, wie man zunächst meinen könnte. Da der Erdumfang am Äquator ca. 40 000 km mißt, ist diese Geschwindigkeit etwa 1667 km/h. Sie beträgt also etwa das zehnfache der Geschwindigkeit eines Mittelklasse-Pkw. Ist der Radius der genannten, vom Verhältnis Impuls zu Drehimpuls abhängigen Kreisbahn größer als der Erdradius, so fliegen die Massen (Stein, Lebewesen, Mensch, Luftmolekül) zwanglos auf einer Kreis- oder Ellipsenbahn (KEPLER-Ellipse) um die ERDE herum. Ist aber der genannte Radius kleiner als der Erdradius, so kommt es zu einem dynamischen Zwangszustand, den wir als Schwerkraft empfinden. Die Größe dieser Schwerkraft ist einerseits davon abhängig, wie groß der Unterschied ist zwischen Erdradius und dem genannten, vom Verhältnis Impuls zu Drehimpuls abhängigen Radius, andererseits davon, wie groß die Masse des betrachteten Körpers ist, was den dynamischen Ursprung der Schwerkraft zusätzlich verdeutlicht. Denn auch die ebenfalls dynamisch bedingte Zentrifugalkraft ist um so größer, je größer die betrachtete Masse ist. Aus der Sicht dieser neuen Interpretation ist die Schwerkraft somit ein qualitativer Nachweis der Erdrotation. Im Rahmen dieser Interpretation muß das 1. Axiom Newtons (nicht mehr: 1. Gesetz) geringfügig abgeändert werden:

1. Axiom  Jeder Körper ohne Drehimpuls beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern

Hierdurch wird eine mehr als 300 Jahre alte, dogmatische Einschränkung aufgehoben und der Weg frei, das Bewegungsverhalten von Körpern mit Drehimpuls zutreffend zu beschreiben. Dieses Bewegungsverhalten ist nämlich im allgemeinen krummlinig (Kreise, Ellipsen usw.). Es ist nicht mehr notwendig, fiktive gravitive Fernwirkungen einzuführen, um krummlinige Bewegungsbahnen verständlich zu machen. Wie in der Arbeit FRIEBE (1996) gezeigt wurde, sind die krummlinigen Bahnen von Himmelskörpern weder abhängig von der Größe einer zentralen Masse noch abhängig von dem Abstand der beteiligten Massen.

Hierdurch wird ferner der Begriff der absoluten Ruhe (beispielsweise: absoluter Raum, physikalischer Raum, Ätherhypothese, Neutrinomeer, Tachyonenfeld, Quantenvakuum) überflüssig. Das Relativitätsprinzip der klassischen Mechanik wird zwanglos anwendbar, wie es EINSTEIN ursprünglich vermutet hatte (vgl. FRIEBE (1996), letzter Absatz).

---

Weitere Links:

THÜRING, B. (1967): „Das Inertial-System“, aus: „Die Gravitation und die philosophischen Grundlagen der Physik“, Verlag Duncker & Humblot, Berlin, Seiten 75 – 77 und 234 – 240

TETENS, H. (1984): „Der Glaube an die Weltmaschine – Zur Aktualität
der Kritik Hugo Dinglers am physikalischen Weltbild“, aus:
Janich, P. (Hrsg.): „Methodische Philosophie – Beiträge
zum Begründungsproblem der exakten Wissenschaften in
Auseinandersetzung mit Hugo Dingler“, Bibliographisches
Institut Mannheim, Wien, Zürich

FRIEBE, E. (1988): „Was sind physikalische Gesetze?“, Zeitschr.
„raum & zeit“, 32/88, S. 88 – 91

FRIEBE, E. (1989): „Sind die Axiome der NEWTON’schen Physik
widerspruchsfrei?“, Zeitschr. „raum & zeit“,
39/89, S. 91 – 94 und DPG-Didaktik-Tagungsband 1989, S. 424 –
429, Hrsg.: Prof. Dr. Wilfried Kuhn, Gießen

HILLE, H. (1995): „Das Realprinzip als Erkenntnisstrategie“,
DPG-Didaktik-Tagungsband 1995, S. 176 – 181. Hrsg.: Deutsche
Physikalische Gesellschaft

FRIEBE, E. (1998): „Das 1. Axiom NEWTONs – Ursache der weltweiten
Krise der Physik“, Vortrag auf der DPG-Frühjahrstagung,
Universität Regensburg, 26. März 1998, Fachverband
Didaktik der Physik

NEUNDORF, W. (1998): „Die Masse – Trägheit und Gravitation“, D – 03054 Cottbus

FRIEBE, E. (1999): „Eine Alternative zur Lösung des Gravitationsproblems“, Vortrag auf der DPG-Didaktik-Frühjahrstagung, Pädagogische Hochschule
Ludwigsburg, am 10. März 1999

FRIEBE, E. (2002): „Gravitation in neuer Sicht“, INTERNET

FRIEBE, E. (2003): „Der Einfluss der Eigenrotation der Planeten auf ihr Bewegungsbahn“, INTERNET

NEUNDORF, W. (2003): „Die Masse – Masse und Raum“, D – 03054 Cottbus

GÖDE WISSENSCHAFTSSTIFTUNG (2004),
Institut für Gravitationsforschung

---

Literatur

---

• Homepage

FRIEBE, Ekkehard (1994): „Die Widerlegung der MAXWELL’schen Elektrodynamik mit Hilfe des Unvollständigkeitssatzes von Kurt GÖDEL“,
DPG-Didaktik-Tagungsband 1994, S. 509 – 514. Hrsg.:
Deutsche Physikalische Gesellschaft (Überarbeitete Fassung vom 22. Oktober 2002

a) Zusammenfassung

Im Jahre 1931 veröffentlichte Kurt GÖDEL den nach ihm benannten Unvoll­ständigkeitssatz. Dieser besagt unter anderem, daß die Widerspruchsfreiheit eines Axiomensystems selbst zu jenen Aussagen gehört, die innerhalb dieses Systems unbeweisbar sind. – Die aus dem Jahre 1865 stammende MAXWELL’sche Elektrodynamik ist vermutlich niemals unter diesem Ge­sichtspunkt untersucht worden. Die diesbezügliche Analyse führt zu dem Ergebnis, daß die MAXWELL’sche Elektrodynamik – unter Einbeziehung ihrer physikalischen Interpre­tation – in sich widersprüchlich und daher in ihren erkenntnis­wissen­schaft­lichen Folgerungen wertlos ist.

Zeichnen, von M. C. Escher (Lithographie, 1948)

Anmerkung: Die Bilder „Zeichnen“ und „Treppauf, Treppab“ sind dem Buch von HOFSTADTER (1992), Seite 734 bzw. Seite 14, entnommen.

b) GÖDELs Unvollständigkeitssatz

Der Unvollständigkeitssatz von Kurt GÖDEL wird allgemeinverständlich und sehr ausführlich besprochen in dem preisgekrönten Buch von HOFSTADTER (1992). Dort heißt es (Zitat von Seite 19, Zeile 2 ff):

„In seiner absolut reinsten Fassung stellt Gödels Entdeckung die Über­setzung einer uralten philosophischen Paradoxie in die Sprache der Mathematik dar. Es handelt sich um die sogenannte Epimenides- oder Lügner-Paradoxie. Epimenides war ein Kreter, der einen unsterblichen Satz aussprach: ,Alle Kreter sind Lügner.‘ Eine verschärfte Version dieser Aussage lautet einfach: ,Ich lüge‘ oder: ,Diese Aussage ist falsch.’“ (Ende des Zitats)

HOFSTADTER führt weiter aus (Zitat von Seite 23, Abs. 3 ff):

„In diesen Paradoxien steckt anscheinend immer der gleiche Haken:
Selbstbezüglichkeit oder „Seltsame-Schleifen-Bildung“. Wenn man sich also das Ziel setzt, alle Paradoxien zu eliminieren, warum versucht man nicht, Selbstbezüglichkeit und alles was dazu führen könnte, zu elimi­nieren? Das ist nicht so leicht wie es scheint, denn unter Umständen ist es schwierig, festzustellen, wo Selbstbezüglichkeit auftritt. Sie kann sich über eine ganze Seltsame Schleife mit verschiedenen Schritten aus­breiten wie in der ,erweiterten‘ Fassung des Epimenides, die an Eschers Zeichnen erinnert: Der folgende Satz ist falsch.
Der vorhergehende Satz ist richtig.“

Treppauf, Treppab, von M. C. Escher (Lithographie, 1960)

„Zusammen haben diese Sätze die gleiche Wirkung wie die ursprüngliche Para­doxie des Epimenides; jeder für sich ist aber harmlos und sogar möglicherweise nützlich. Die ,Schuld‘ für diese Seltsame Schleife kann nicht einem der beiden Sätze zugeschrieben werden, sondern nur der Art, wie sie gegenseitig aufeinander verweisen. Gleichermaßen ist der lokale Einzelteil von Treppauf, Treppab durchaus legitim, erst die Art und Weise, wie sich die Teile zu einem globalen Ganzen zusammenfügen, schafft etwas Unmögliches. Da es direkte und indirekte Möglichkeiten gibt, Selbstbezüglichkeit herzustellen, muß man ausfindig machen, wie man beide Arten gleichzeitig eliminieren kann – wenn man in der Selbstbezüglichkeit die Wurzel allen Übels sieht.“ (Ende des Zitats)

In diesem Zusammenhang sind noch folgende Aussagen von HOFSTADTER wichtig (Zitate von Seite 103, vorletzter Absatz, bis Seite 104, erster Absatz):

„Es zeigt sich nunmehr, daß Widerspruchsfreiheit nicht eine Eigenschaft eines formalen Systems als solchen, sondern von der dafür vor­ge­schla­ge­nen Interpretation abhängig ist. Aus dem gleichen Grund ist Wider­sprüch­lich­keit keine intrinsische Eigenschaft irgendeines for­malen Systems.“ „Nun aber wollen wir genau sagen, was man unter Widerspruchsfreiheit eines formalen Systems (zusammen mit einer Interpretation) versteht: daß jeder SATZ, wenn interpretiert, zu einer wahren Aussage wird. Und wir werden sagen, daß Widersprüchlichkeit dann vorliegt, wenn sich unter den interpretierten SÄTZEN zumindest eine falsche Aussage befindet.“ (Ende der Zitate)

c) MAXWELLs Elektrodynamik

Die Elektrodynamik von MAXWELL (1865) ist seit ihrer ersten Formulierung vielfach verändert worden. Ihre Kernaussage ist aber stets die gleiche geblieben und findet ihren Ausdruck in den folgenden Gleichungen. Man nennt sie auch die homogenen Gleichungen der MAXWELL’schen Elektrodynamik:

Dabei sind Õ₀ und Ü₀ – gemäß Voraussetzung – von Ort und Zeit unabhängige Konstanten, aus denen nach Lehrbuchaussagen die Vakuum-Lichtgeschwindigkeit c errechnet werden kann. Der Operator ‚rot‘ in den vorstehenden Gleichungen stellt in bekannter Weise eine spezielle Differentiation nach drei Raumkoordinaten dar.

Mit dem Begriff ,“Raum“ im Zusammenhang mit den drei Raumkoordinaten ist schon eine erste Interpretation verbunden. Wie jedoch HOFSTADTER ausführt [siehe Abschnitt b) vorliegender Arbeit], ist aufgrund der von GÖDEL formulierten Erkenntnis streng zu unterscheiden zwischen dem rein formalen, mathematischen System, das in vielen Fällen nicht zu entscheiden gestattet, ob Widerspruchsfreiheit vorliegt oder nicht, und dem interpretierten System, aufgrund dessen erst Widersprüche erkennbar werden.

Die Glgn. (1) und (2) lassen erkennen, daß sie gegenseitig aufeinander verweisen. Denn das E auf der rechten Seite von GIg. (1) tritt in GIg. (2) links wieder auf. In gleicher Weise tritt das H der rechten Seite von GIg. (2) in GIg. (1) links wieder auf.

In dem System der Glgn. (1) und (2) ist – bei Fortfall jeglicher Interpretation – ein Widerspruch nicht ersichtlich. Auch eine Betrachtung der ,erweiterten‘ Fassung des Epimenides (siehe oben):

Der folgende Satz ist falsch.
Der vorhergehende Satz ist richtig.

bringt uns hier nicht weiter. Denn bei keiner der beiden Gleichungen (1) und (2) wird unterstellt, daß eine von ihnen falsch sei. Denn beide gelten als experimentell bestens bestätigt. Das ist auch der Grund, warum die MAXWELL’schen Gleichungen von Theoretikern immer wieder überprüft und für widerspruchsfrei befunden wurden, während die Kritik schon seit vielen Jahren darauf hinweist, daß hierbei doch irgend etwas nicht stimmen könne.

Besonders deutlich hat Ivor CATT (1980) eine diesbezügliche Kritik ausge­sprochen. Er kommt nach eingehenden Untersuchungen zu dem Ergebnis (aus dem Englischen übersetztes Zitat aus der Arbeit CATT 1980, S.77, letzter Abs., bis S.78, erster Abs.):

„Es ist schockierend, daß dieser Unsinn ein Jahrhundert lang als die für die elektromagnetische Theorie entscheidende Kernaussage überlebt hat. Wir erkennen, daß die mathematische Formulierung der elektromagnetischen Theorie – weit entfernt davon, den Gegenstand exakter zu machen – diese lächerlich und falsch gemacht hat. Wir sehen, daß die Mathematiker inkompetent sind dort, wo die physikalische Wirklichkeit beteiligt ist. Sie verbergen ihre lnkompetenz und verwirren andere durch das Heraufbeschwören von unsinnigen diesbezüglichen Formeln.“ (Ende des Zitats)

Dieser Aussage kann im wesentlichen zugestimmt werden; dennoch ist – wie Diskussionen ergeben haben – die mathematische Begründung von CATT hierzu fehlerhaft. Denn die von CATT behauptete Widersprüchlichkeit ist – den Aussagen von GÖDEL und HOFSTADTER entsprechend – innerhalb des formalen mathematischen Systems selbst nicht nachweisbar. Eine diesbezügliche Entscheidung ist deshalb nur aus der physikalischen Problematik heraus zu fällen. Dies soll im folgenden näher erläutert werden.

Für die Aufstellung der MAXWELL’schen Gleichungen kam dem Induktionsgesetz nach FARADAY eine besondere Bedeutung zu. Denn MAXWELL waren die umfangreichen Versuchsergebnisse von FARADAY bereits be­kannt. Die mathe­matische Beschreibung des Induktionsgesetzes durch die GIg. (2) hat sich seit vielen Jahrzehnten hervorragend bewährt. Es wird in der Fachliteratur zutreffend und sehr ausführlich behandelt.

Zur Formulierung der GIg. (1) dagegen führte MAXWELL – in Ermangelung experimenteller Ergebnisse – die Hypothese vom Verschiebungsstrom (displacement current) ein. Diese besagt, daß nicht nur – wie damals schon bekannt – Ströme in elektrischen Leitern von magnetischen Feldlinien, sondern daß auch zeitlich veränderliche elektrische Felder (vgl. rechte Seite der GIg. 1) von eben solchen magnetischen Feldlinien umgeben seien. Durch die sehr ausführlichen Untersuchungen von CATT (1978,1979) – in Verbindung mit CATT (1984) und CATT (1985) – ist inzwischen gezeigt worden, daß diese MAXWELL’sche Hypothese – entgegen einer weitverbreiteten Meinung – nicht der physikalischen Realität entspricht. Das eingehende Studium dieser Arbeiten von CATT wird empfohlen. Es ergibt sich daher, daß die GIg. (1) ersatzlos zu streichen ist [siehe: FRIEBE (1995)]. Zur Lichtgeschwindigkeit c ist eine theoretische Aussage nicht mehr möglich, da diese die Existenz zweier Gleichungen voraussetzt.

Eine weitere physikalische Problematik liegt vor allem in folgendem:

Aufgrund der Tatsache, daß die Größen Õ₀ und Ü₀ in der Literatur als Naturkon­stanten des leeren RAUMES (Vakuums) interpretiert wurden, ordnete man dem leeren RAUM, dem Vakuum, dem NICHTS physikalische Eigenschaf­ten zu [siehe: FRIEBE (2001/1988)]. Diese Zuordnung ist vergleichbar mit dem Begriff des absoluten Raumes in der NEWTON’schen Bewegungslehre. Aus dieser Zuordnung ergab sich die Folgerung einer absoluten Konstanz der Lichtgeschwindigkeit. Diese ist aber weder mit der Annahme eines Lichtmediums (Äthers) noch mit dem klassischen Relativitätsprinzip vereinbar, wie vor allem GUT (1981) überzeugend dargelegt hat. Außerdem ist die Be­hauptung einer absoluten Konstanz der Lichtgeschwindigkeit auch experi­mentell bereits widerlegt [siehe FRIEBE (1992)]. Es ergibt sich also, daß die MAXWELL’sche Elektrodynamik – unter Einbeziehung ihrer physikalischen Interpre­tation – in sich widersprüchlich und daher in ihren erkenntniswissenschaftlichen Folgerungen wertlos ist.

d) Literatur

CATT, I. (1978): „Displacement Current“ „Wireless World“, December 1978, p. 51 – 52

CATT, I. (1979): „The History of Displacement Current“ „Wireless World“, March 1979, p. 67 – 68

CATT, I. (1980): „Maxwell’s equations revisited“, „Wireless World“, March 1980, p. 77 – 78

CATT, I. (1984): „Fundamentals of electromagnetic energy transfer“, „Electronics & Wireless World“, Sept. 1984, p. 45 – 48, and Oct. 1984, p. 50 – 51

CATT, I. (1985): „The hidden message in Maxwell’s equations“, „Electronics & Wireless World“, Nov. 1985, p. 35 – 36, and Dec. 1985, p. 33, 34, 75

FRIEBE, E. (1992): „Das Dogma der Lichtgeschwindigkeit als Grenzgeschwin­dig­keit“, DPG-Didaktik-Tagungsband 1992, S. 552 – 555. Hrsg.: Deutsche Physika­lische Gesellschaft

FRIEBE, E. (1995): „Die Vektorprodukte der MAXWELL’schen Elektrodynamik“, DPG-Didaktik-Tagungsband 1995, S. 394 – 399. Hrsg.: Deutsche Physikalische Gesellschaft

FRIEBE, E. (2001): „Sind Dielektrizität und Permeabilität des Vakuums Natur­kon­stanten?“, (gekürzte und überarbeitete Fassung aus FRIEBE (1988): „Was sind physikalische Gesetze?“, Zeitschrift „raum & zeit“, 32/88, S. 88 – 91)

GÖDEL, K. (1931): „Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I.“, Monatshefte für Mathematik und Physik, Bd. 38, S.173 – 198

GUT, B. (1981): „Immanent-logische Kritik der Relativitätstheorie“, Verlag Rolf Kugler, CH-6317 Oberwil b. Zug, Schweiz

HOFSTADTER, D. R. (1992): „Gödel, Escher, Bach – ein Endloses Geflochtenes Band“, 2. Aufl., Klett-Cotta im Deutschen Taschenbuch Verlag

MAXWELL, J. C. (1865): „A Dynamical Theory of the Electromagnetic Field“, Philosoph. Transactions, London, p. 459 – 512

Homepage

FRIEBE, Ekkehard (1998):
„Das 1. Axiom NEWTONs – Ursache der weltweiten Krise der Physik“,
Vortrag auf der DPG-Frühjahrstagung, Universität
Regensburg, 26. März 1998,
Fachverband Didaktik der Physik

.

a) Zusammenfassung

Die Theoretische Physik rechnet so, als ob das 1. Axiom von Isaac NEWTON ( – Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern – ) ein allgemeingültiges Naturgesetz sei, obwohl ein Axiom lediglich eine Festsetzung darstellt. Die mathematische Ableitung zum sogenannten NEWTON-schen Gravitationsgesetz geht von diesem Axiom aus und kommt zu der irrtümlichen Behauptung von gravitiven Anziehungskräften (Fernwirkung) zwischen den Himmelskörpern.

Hierin hat die weltweite Krise der Theoretischen Physik ihren eigentlichen Ursprung.

b) Die linear-gleichförmige Bewegung

Betrachtet man die eingangs gebrachte Grafik der Wanderung der Erde um die Sonne, so erkennt man beispielhaft folgende drei Eigenschaften der Planeten des Sonnensystems:

a) Der Planet läuft auf einer gekrümmten Bahn um die Sonne herum.

b) Der Planet rotiert um seine eigene Achse (Rotationsachse).

c) Die Rotationsachse besitzt gegen die Ebene der Umlaufbahn eine Neigung, die im Zyklus über Frühling, Sommer, Herbst, Winter laufend anders gegenüber der Bahnebene orientiert ist.

Als Isaac NEWTON seinerzeit das nach ihm benannte „Gravitationsgesetz“ formulierte, zog er nur die Eigenschaft a) in Betracht, vernachlässigte aber – aus welchen Gründen auch immer – die Eigenschaften b) und c). Er ging anstatt dessen von der auf GALILEI zurückgehenden Annahme aus:

Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.

Diese Annahme wird heute als das 1. Axiom von Isaac NEWTON bezeichnet. Deshalb wird vielfach angenommen, dieses Axiom sei erstmals von Newton selbst formuliert worden. Das ist nicht der Fall. Newton selbst schreibt, nachdem er zuvor seine Prinzipien und Zusätze formuliert hat, folgendes (Zitat aus NEWTON 1963, S. 39, 3. Abs.):

Anmerkung: Bis jetzt habe ich die Principien dargestellt, welche von den Mathematikern angenommen, und durch vielfältige Versuche bestätigt worden sind. Durch die zwei ersten Gesetze und die zwei ersten Zusätze fand GALILEI, dass der Fall schwerer Körper im doppelten Verhältnis der Zeit stehe, und dass die Bewegung der geworfenen Körper in Parabeln erfolge; übereinstimmend mit der Erfahrung, in so weit jene Bewegungen nicht durch den Widerstand der Luft etwas verzögert werden. (Ende des Zitats)

Lange Zeit wurde das genannte 1. Axiom als universell gültiges Naturgesetz angesehen. So schreibt beispielsweise Roger COTES in seiner Vorrede aus dem Jahre 1713 zur zweiten Ausgabe von Newtons „Mathematische Principien der Naturlehre“ (Zitat aus NEWTON 1963, S. 6, vorletzter Abs.):

Dass jeder Körper in seinem Zustande der Ruhe, oder der gleichförmigen geradlinigen Bewegung verharre, wofern er nicht durch einwirkende Körper gezwungen wird, jenen Zustand zu verändern, ist ein von allen Gelehrten angenommenes Naturgesetz. Hieraus folgt aber, dass Körper, welche sich in Curven bewegen, also von den ihre Bahnen berührenden geraden Linien beständig abweichen, durch irgend eine fortwährend wirkende Kraft in ihrer krummlinigen Bewegung zurückgehalten werden. Da die Planeten sich in krummen Bahnen bewegen, muss nothwendig irgend eine Kraft da sein, durch deren wiederholte Wirksamkeit sie unaufhörlich von ihren Tangenten abgelenkt werden. (Ende des Zitats)

Die linear-gleichförmige Bewegung wird also hier als naturgesetzlich angenommen, obwohl noch nie jemand in der unbeeinflußten Natur eine solche Bewegung beobachtet hat. Wirft man z. B. einen Körper senkrecht in die Höhe, so bewegt er sich zwar linear aber nicht gleichförmig. Wirft man ihn dagegen in horizontaler oder in schräger Richtung, so bewegt er sich weder gleichförmig noch linear (GALILEI-Parabel). Die Schwerkraft ist die Ursache.

Es bleibt also die Frage, ob die linear-gleichförmige Bewegung bei Fortfall der Schwerkraft eine naturgesetzliche Bewegung ist?

Nein! Dies ist nicht der Fall. Neuere Erkenntnisse zeigen nämlich, daß Körper mit Rotation (Drehimpuls) krummlinige Bahnen beschreiben. Die Vernachlässigung der Rotation der Planeten durch NEWTON muß daher aus heutiger Sicht als eine wesentliche Ursache der weltweiten Krise der Theoretischen Physik angesehen werden.

c) Kosmische Beschleunigungen

Die meisten Naturwissenschaftler glauben, daß beschleunigte Bewegungen – auch Drehbewegungen (Rotationen) sind beschleunigte Bewegungen – bezüglich der Bezugssysteme einen anderen Rang einnehmen als linear-gleichförmige Bewegungen. Dieses ist ein altes Dogma, das auf NEWTONs Zeit zurückgeht, und zwar auf NEWTONs DEFINITION:

Kraft = Masse mal Beschleunigung.

(Vergleiche hierzu: NEUNDORF (1998):  „Der Massenbegriff – Beispiel eines der undefiniert verwendeten Begriffe in der Physik“)

Befindet sich beispielsweise ein Körper A vollkommen allein im weiten Kosmos, so kann ihm – mangels eines geeigneten Bezugs – keine Beschleunigung zugeschrieben werden, nicht einmal die Beschleunigung NULL. Kommt aber ein zweiter Körper B hinzu, so kann durch Beobachtung (oder durch optische Messung) festgestellt werden, ob beide Körper relativ zueinander beschleunigt sind. Die Beobachtung (oder optische Messung) selbst kann aber – sofern keine weiteren Informationen zur Verfügung stehen – nicht entscheiden, ob Körper A oder Körper B beschleunigt ist oder ob beide Körper anteilig beschleunigt sind. Dasselbe gilt natürlich auch für negative Beschleunigungen (Verzögerungen).

Es ergibt sich also für jeden, ggf. rotierenden Beobachter (Meßvorrichtung, Bezugssystem) ein anderer Wert der Beschleunigung. Eine Beschleunigung ist deshalb keine „Eigenschaft“ eines einzelnen Objektes sondern eine Relation, die nur zwischen mindestens zwei Objekten einen Sinn ergibt.

Dennoch ist ein beschleunigtes (oder verzögertes) Geschoß oder ein beschleunigt (oder verzögert) fahrendes Auto keine rein theoretische Angelegenheit, sobald die Möglichkeit eines Zusammenstoßes zweier Objekte besteht. Der Zerstörungseffekt, der beim Zusammenstoß beider Objekte entsteht, ist aber weder vom Standpunkt und/oder vom Bewegungszustand eines außerhalb befindlichen Beobachters noch von irgend einem Bezugssystem abhängig, sondern nur von der Relativbeschleunigung beider Objekte relativ zueinander im Augenblick des Zusammenstoßes.

Es sind also grundsätzlich zwei Arten von Beschleunigungen zu unterscheiden:

a) Beschleunigungen als Relationen in Bezug auf einen Beobachter (Meßeinrichtung, Bezugssystem).

b) Beschleunigungen als Relativbeschleunigungen zwischen zwei miteinander reagierenden Objekten.

Die klassische Physik hat diesen Unterschied nicht gesehen und deshalb beide Arten von Beschleunigungen in ihren mathematischen Konzepten in unzulässiger Weise miteinander verknüpft.

Schon frühzeitig hat Hugo DINGLER diesen Sachverhalt erkannt. In seinem Buch: „Physik und Hypothese“ (1921) schreibt er im Abschnitt: „Kritische Analyse der Grundlagen der Relativitätstheorie“ (Zitat aus DINGLER 1921, S. 153 bis 154):

Der in Translation begriffene Eisenbahnwagen erleide nun eine Beschleunigung. Was wird geschehen? Sollte ich gerade beim Ballspielen sein, so werde ich selbst Mühe haben, mich aufrecht zu erhalten, indem ich mich am nächsten Gegenstande festhalte. Mein in der Luft befindlicher Ball wird nicht mehr am gleichen Platz herabfallen. „Also ist eine Beschleunigung bemerkbar“, schließt man. Bei dieser passierte doch offenbar folgendes: Die Beschleunigung wurde ausgeübt zuerst auf die Puffer oder den Verbindungshaken des Wagens. Von diesen verbreitete sie sich auf die mit diesen in fester Verbindung befindlichen Teile, darunter schließlich auch auf meine Füße. Da aber mein Oberkörper mit diesen nicht in völlig fester Verbindung steht, so kam der nicht gleich mit und fiel um. Ebenso war es mit dem Ball. Es ist also gar nicht wahr, daß auf das ganze System eine Beschleunigung ausgeübt wurde. Auf einen Teil des Systems nur, der zufällig die anderen durch seine Form räumlich umschließt, wurde eine Beschleunigung ausgeübt. Bei der Translation wird stillschweigend angenommen, daß alle Teile des Systems sie haben; hier ist nur ein Teil beschleunigt, andere nicht, und lediglich dieser Unterschied in der Behandlung der verschiedenen Teile des Systems wird wahrgenommen, sonst nichts. Denken wir uns statt der Lokomotive als Bewegungserzeugung einen großen Körper in größerer Entfernung der in der Bewegungsrichtung den Wagen und alle Körper attrahiert, ihnen also Beschleunigungen erteilt, dann ist von diesen ebensowenig auf mechanischem Wege zu bemerken, wie von einer Translation. Alle Körper, Wagen und Inhalt erhalten die gleichen Beschleunigungen, und relativ zu einander bleibt alles beim alten. Dabei könnte das Attraktionsgesetz noch beliebig von der Zeit abhängen. (Ende des Zitats)

Die Kraft, die z. B. ein Sportler bei der Sportdisziplin Kugelstoßen aufbringen muß, kann er nur erbringen, indem er sich auf dem Erdboden abstützt. Das Prinzip

actio = reactio

wird hier wirksam. Die NEWTON zugeschriebene Beziehung

Kraft = Masse mal Beschleunigung

suggeriert, es sei nur eine Masse an dem jeweils betrachteten Vorgang beteiligt. In Wirklichkeit ist aber der Planet ERDE mit im Spiel, für den stillschweigend die

Masse = UNENDLICH

vorausgesetzt ist. Diese Voraussetzung schließt die Annahme ein, daß die ERDE die Beschleunigung NULL aufweist. Damit ist für die klassische Mechanik (mit Ausnahme der Himmelsmechanik) zwangsläufig die ERDE das Bezugssystem für Beschleunigungen.

Betrachtet man jedoch solche Zuordnungen, bei denen auch die abstützende, zweite Masse ungleich unendlich ist, dann wird deutlich, daß stets die Relativbeschleunigung beider Massen relativ zueinander entscheidend ist. Diese Relativ-beschleunigung erzeugt beispielsweise der kugelstoßende Sportler durch seine Muskelkraft, die er zwischen Kugel und abstützender Masse aufbringt. Als Beispiel sei das Kugelstoßen von einem leicht beweglichen Boot aus genannt. Außenstehende Beobachter oder Bezugssysteme haben keinen Einfluß auf den physikalischen Vorgang.

Alternativ ist hier der Raketenantrieb zu nennen, dessen abstützende Masse durch eine Vielzahl kleiner Teilchen gebildet wird, die zum einen häufig nicht direkt sichtbar sind und die zum anderen keinen einheitlichen Ort und keine einheitliche Geschwindigkeit aufweisen. In keinem Falle ist jedoch der sogenannte absolute Raum das universelle Bezugssystem.

d) Abänderung des 1. Axioms NEWTONs

In der Arbeit FRIEBE (1997) wurde aufgezeigt, daß – zur Berücksichtigung des Drehimpulses – das 1. Axiom NEWTONs nur geringfügig abgeändert werden muß, und zwar wie folgt (Zitat):

1. Axiom
Jeder Körper ohne Drehimpuls beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern. Hierdurch wird eine mehr als 300 Jahre alte, dogmatische Einschränkung aufgehoben und der Weg frei, das Bewegungsverhalten von Körpern mit Drehimpuls zutreffend zu beschreiben.

Dieses Bewegungsverhalten ist nämlich im allgemeinen krummlinig (Kreise, Ellipsen usw.). Es ist nicht mehr notwendig, fiktive gravitive Fernwirkungen einzu-führen, um krummlinige Bewegungsbahnen verständlich zu machen. Wie in der Arbeit von FRIEBE (1996) gezeigt wurde, sind die krummlinigen Bahnen von Himmelskörpern weder abhängig von der Größe einer zentralen Masse noch abhängig von dem Abstand der beteiligten Massen.

Hierdurch wird ferner der Begriff der absoluten Ruhe (beispielsweise: absoluter Raum, physikalischer Raum, Ätherhypothese, Neutrinomeer, Tachyonenfeld, Quantenvakuum) überflüssig. Das Relativitätsprinzip der klassischen Mechanik wird zwanglos anwendbar, wie es EINSTEIN ursprünglich vermutet hatte. (Ende des Zitats)

e) Schwerkraft als dynamische Kraft

In diesem Zusammenhang tritt sogleich folgende Frage auf:

Wie erklärt sich die auf der Erdoberfläche feststellbare Schwerkraft, wenn keine Kräfte zwischen den Himmelskörpern vorhanden sind?

Betrachten wir hierzu (fiktive) Himmelskörper, welche die ERDE umkreisen – ähnlich dem irdischen Mond. Die Massen dieser Himmelskörper bewegen sich aufgrund ihres mitgeführten Drehimpulses auf einer vergleichsweise großen Kreisbahn. Der Radius dieser Kreisbahn ist abhängig von dem Verhältnis Impuls zu Drehimpuls. Ist dieser Radius größer als der Erdradius, so bewegen sich die Massen zwanglos auf einer Kreis- oder Ellipsenbahn (KEPLER-Ellipse) um die ERDE herum. Ist aber der genannte Radius kleiner als der Erdradius, so kommt es zu einem dynamischen Zwangszustand, den wir als Schwerkraft empfinden.

Die Größe dieser Schwerkraft ist einerseits davon abhängig, wie groß der Unterschied ist zwischen Erdradius und dem genannten, vom Verhältnis Impuls zu Drehimpuls abhängigen Radius, andererseits davon, wie groß die Masse des betrachteten Körpers ist. Unter diesem Aspekt wird auch die „Äquivalenz“ von träger und schwerer Masse zu einer logischen Notwendigkeit. Außerdem ist im Rahmen dieser neuen Interpretation die Schwerkraft ein qualitativer Nachweis der Erdrotation. – Diese Gedanken wurden schon in den Arbeiten FRIEBE (1996) und FRIEBE (1997) erläutert.

f) Weitere Fragen zum abgeänderten 1. Axiom

Seit Erscheinen der Arbeiten FRIEBE (1996)  und FRIEBE (1997) sind noch folgende Fragen aufgetreten:

1. Ist das neu formulierte 1. Axiom ein echtes Naturgesetz?

2. Wie erhält man den krummlinigen Bahnverlauf eines
Himmelskörpers, obwohl das abgeänderte 1. Axiom eine Negativaussage (ohne Drehimpuls) beinhaltet?

3. Wie können mit diesem Modell elliptische Bahnformen der Himmelskörper erklärt werden?

4. Wie erklärt es sich, daß einzelne Planeten rückläufig rotieren?

5. Ist das „Inertialsystem“ eine zweifelsfreie Basis zur mathematischen Beschreibung von kosmischen Geschwindigkeiten und Beschleunigungen?

Zu 1:
Nein! Denn im Kosmos ist der Begriff einer geradlinigen Bewegung überhaupt nicht definiert. Denn die Erde und vermutlich alle anderen Himmelskörper drehen sich um ihre eigene Achse, so daß abhängig davon, wo sich ein Beobachter (oder eine optische Meßvorrichtung) befindet, ein und dieselbe Bewegung – aufgrund der Eigenrotation des Beobachters (oder der Meßvorrichtung) – als geradlinig oder krummlinig zu beschreiben ist, und zwar unabhängig davon, ob man einen „absolut ruhenden Raum“ als gegeben annimmt oder nicht. Eine geradlinige Bewegung läßt sich daher nur in Bezug auf einen einzigen Himmelskörper und dessen Rotationsverhalten eindeutig definieren. Das neue 1. Axiom gilt daher – ebenso wie das 1. Axiom NEWTONs – nur in einem beschränkten Bereich als erste Näherung; vgl. FRIEBE (1989), Abschnitt A.

Zu 2: Ein Himmelskörper kann als starrer Körper betrachtet werden, der aus einer Vielzahl von mechanisch fest miteinander verbundenen Punktmassen besteht, die selbst – wegen ihrer differentiell kleinen Abmessungen – ohne Drehimpuls sind. Ein bewegter Körper mit Drehimpuls ist bereits durch mindestens zwei gleiche, mit Abstand starr miteinander verbundene Punktmassen P und Q darstellbar, die um den gedachten (fiktiven, masselosen) Schwerpunkt S rotieren (siehe BILD, die geradlinigen Pfeile deuten Geschwindigkeits- vektoren zum Zeitpunkt t = 0 an, der krummlinige, ausgezogene Pfeil kennzeichnet den Drehsinn).

Bei Anwendung des abgeänderten 1. Axioms auf beide Punktmassen unter Berücksichtigung ihrer Einzel-geschwindigkeiten (Anteile der rotierenden und der linear-gleichförmigen Bewegung) ergeben sich über die starre Verbindung von P und Q Trägheitskräfte, die eine geradlinige Bewegung des Schwerpunktes S verhindern. Es folgt eine Bewegungsbahn von S entsprechend dem krummlinigen, punktierten Pfeil im BILD (Computer-Simulation).

Zu 3:
Wir gehen zunächst davon aus, daß die Umlaufbahn des zu betrachtenden Himmelskörpers in einer Ebene verläuft. Die Ursache der elliptischen Bahnform ist nun die Neigung der Rotationsachse gegen die Bahnebene. Dabei ist zu berücksichtigen, daß diese Neigung im Zyklus über Frühling, Sommer, Herbst, Winter laufend anders gegenüber der Bahnebene orientiert ist. Zur weiteren Analyse kann man den Rotations-Vektor in drei Komponenten zerlegen:

Komponente A senkrecht zur Bahnebene;

Komponente B parallel zur Bahnebene parallel zur
Bewegungsbahn;

Komponente C parallel zur Bahnebene senkrecht zur
Bewegungsbahn.

Die Komponente A bewirkt eine kreisförmige Bahn (siehe oben).

Die Komponente B bewirkt eine Richtungsstabi-lisierung in Richtung der Bewegungsbahn, wie beispielsweise bei Artilleriegeschossen mit Drall.

Die Komponente C erzwingt eine Krümmung der sogenannten Bahnebene.

Ist die Komponente A allein vorhanden, so ist nur eine kreisförmige Bahn möglich. Wie die eingangs gebrachte Grafik: Wanderung der Erde um die Sonne erkennen läßt, bleibt der Betrag der Komponente A während eines Umlaufes unverändert. Die Komponente B ändert während eines Umlaufes ihren Wert von einem positiven Maximum über Null zu einem negativen Maximum. Da die richtungsstabilisierende Wirkung vom Vorzeichen unabhängig ist (es ist z. B. bei Artilleriegeschossen mit Drall gleichgültig, ob Linksdrall oder Rechtsdrall vorliegt), interessiert nur der Betrag. Die Komponente C ändert ebenfalls während eines Umlaufes ihren Wert von einem positiven Maximum über Null zu einem negativen Maximum. Hier bewirkt das wechselnde Vorzeichen eine Krümmung der sogenannten Bahnebene das eine Mal zur einen Seite, das andere Mal zur anderen Seite, so daß eine gewellte Ebene die Folge ist. Die Behauptung einer Bahnebene ist daher lediglich eine Näherung. Der elliptische Bahnverlauf resultiert aus dem Wechselspiel der Komponenten A und B. Aber auch die gewellte Ebene gemäß Komponente C kann zusätzlich einen nicht-kreisförmigen Bahnverlauf verursachen.

Zu 4:
Von den Planeten Merkur, Venus, Erde, Mars, Jupiter, Saturn, Uranus, Neptun rotieren nur Venus und Uranus rückläufig. Diese beiden Planeten haben aber – als einzige – eine Achsneigung größer als 90 Grad, und zwar 117,3 Grad (Venus) und 97,87 Grad (Uranus), was dynamisch gleichbedeutend ist mit einer vorwärtsläufigen Rotation von 180 – 117,3 = 62,7 Grad (Venus) und 180 – 97,87 = 82,13 Grad (Uranus).

Zu 5:
Nein! Das Inertialsystem ist die Ursache vieler Mißverständnisse, da es auf der linear-gleichförmigen Bewegung aufbaut. Lesen Sie hierzu: THÜRING (1967), S. 75 bis 77 und S. 234 bis 240.

Ein Hauptanliegen der vorstehenden Untersuchung ist es, neue Denkanstöße zu geben und uralte Dogmen abzubauen. Folgende Dogmen, die eng miteinander verknüpft sind, stehen dabei im Vordergrund:

1. Der Glaube an die Weltmaschine (vgl. TETENS 1984).
2. Der Glaube an den absoluten Raum als universelles Bezugssystem.
3. Der Glaube an gravitive Fernwirkungen.

Durch Überwindung dieser Dogmen wird ein neues Verständnis der Weltraumfahrt möglich. Mit dem abgeänderten 1. Axiom wird die Äquivalenz von träger und schwerer Masse zur Selbstverständlich- keit, da die Schwerkraft auf der Erdoberfläche aufgrund einer rotierenden trägen Masse (Drehimpuls) rein dynamisch begründet ist.

Literatur:

DINGLER, H. (1921): „Physik und Hypothese – Versuch einer induktiven Wissenschaftslehre nebst einer kritischen Analyse der Fundamente der Relativitätstheorie“, Verlag Walter de Gruyter, Berlin und Leipzig

FÖLSING, A. (1984): „Der Mogelfaktor – Die Wissenschaftler und die Wahrheit“, Verlag Rasch und Röhring, Hamburg

FRIEBE, E. (1999): „Die Gleichheit der trägen und schweren Masse“, Vortrag auf der DPG-Didaktik-Frühjahrstagung, Pädagogische Hochschule Ludwigsburg, am 10. März 1999

JAMMER, M. (1964): „Der Begriff der Masse in der Physik“, Wissenschaftliche Buchgesellschaft, Darmstadt

NEWTON, I. (1963): „Mathematische Prinzipien der Naturlehre“, mit Bemerkungen und Erläuterungen. Herausgegeben von J. Ph.

WOLFERS. Mit einer Vorrede von Roger Cotes aus dem Jahre 1713. Wissenschaftliche Buchgesellschaft, Darmstadt.

ROSENBERGER, F.(1895): „Isaac Newton und seine Physikalischen Principien – Ein Hauptstück aus der Entwicklungsgeschichte der modernen Physik“, Johann Ambrosius Barth, Leipzig – Reprint
1978: Unveränderter Nachdruck der Ausgabe Leipzig 1895, Dr. Martin Sändig GmbH, Walluf, Nendeln

TETENS, H. (1984): „Der Glaube an die Weltmaschine – Zur Aktualität der Kritik Hugo Dinglers am physikalischen Weltbild“, aus: Janich, P. (Hrsg.): „Methodische Philosophie – Beiträge zum Begründungsproblem der exakten Wissenschaften in Auseinandersetzung mit Hugo Dingler“, Bibliographisches Institut Mannheim, Wien, Zürich

THÜRING, B. (1967): „Die Gravitation und die philosophischen Grundlagen der Physik“, Verlag Duncker & Humblot, Berlin

---

• Homepage

FRIEBE, Ekkehard (1996): „Newtons Gravitationsgesetz . . . . .
nur die halbe Wahrheit?“,
DPG-Didaktik-Tagungsband 1996. Hrsg.: Deutsche Physikalische Gesellschaft

————————————————————————————————-

a) Zusammenfassung

Unter vorstehendem Titel erschien in der Zeitschrift „bild der wissenschaft“, 1989, H. 3/89, S. 49 – 58, ein Aufsatz der Autoren H. J. FAHR und W. KNAPP. Diese Arbeit enthält als Untertitel die Fragestellung: „. . . rechnen wir seit Jahrhunderten falsch?“ Diese letztgenannte Fragestellung muß eindeutig mit „JA“ beantwortet werden, wie eine Untersuchung anhand des Tagungsbandes zum „Ersten internationalen Kongreß für Relativität und Gravitation, München 1988“ in Verbindung mit weiteren Recherchen ergeben hat. Die Ursache liegt in NEWTONS 1. Axiom: „Kräftefreie physikalische Körper befinden sich stets im Zustande der Ruhe oder der gleichförmig-geradlinigen Bewegung.“ Dies ist eine einschränkende Axiomatik, die nur auf Punktmassen oder nicht punktförmige, reale Körper ohne Drehimpuls anwendbar ist. Reale Körper mit Drehimpuls bewegen sich im allgemeinen auf krummlinigen Bahnen, abhängig von Betrag und Richtung des Drehimpuls-Vektors. Attraktionskräfte nach dem NEWTON’schen Gravitationsgesetz erweisen sich als Fiktionen, die mit der Realität unvereinbar sind. Maßgebend für die Bewegung von kräftefreien Himmelskörpern sind Anfangs-Impuls und Anfangs-Drehimpuls.

b) Erster Internationaler Kongreß für Relativität und Gravitation, München

Vom 22. – 24. April 1988 fand in München der „Erste internationale Kongreß für Relativität und Gravitation“ statt. Die Veranstaltung war von Herrn Emil Andrej Maco angeregt, organisiert und vorbereitet worden. Außerdem war sie durch eine Pressekonferenz am 6. 11. 1987 im Hotel Sheraton, Frankfurt/M., und durch ein Pressegespräch am 10. 12. 1987 im Hotel Hilton, München, bekanntgemacht worden. Die Resonanz der Presse war nahezu Null. Lediglich die Zeitschrift „raum & zeit“, Ehlers-Verlag München/Sauerlach, die den Kongreß mit initiiert hatte, berichtete ausführlich, vor und nach der Tagung. Auch nach dem eigentlichen Kongreß hüllte sich die Presse (mit Ausnahme von „raum & zeit“) in Schweigen, obwohl Journalisten geladen und auch erschienen waren.

Dabei wurden auf diesem Kongreß ganz wesentliche Erkenntnisse diskutiert, die einer sensations-hungrigen Presse genügend Zündstoff geliefert hätten:

Emblem des Kongresses

.
Grundlegende Irrtümer der auf NEWTON zurückgehenden Gravitationstheorie, der EINSTEIN zugeschriebenen speziellen Relativitätstheorie und der von EINSTEIN entwickelten Gravitationstheorie (sogenannte allgemeine Relativitätstheorie).

Im November 1988 kam der Tagungsband zu diesem Kongreß heraus, zusammengestellt und bearbeitet von Herrn Emil Andrej Maco. Auf dem Titelblatt sind folgende Themen aufgeführt (Zitat):

„ 1. Widerlegung der Relativitätstheorie 2. Schaffung einer neuen, zeitgemäßen Physik 3. Progressive Ideen auf dem Gebiet der Gravitation.“

Als Zielsetzung wird u. a. genannt (Zitat):

„Der Weg aus der Relativität führt nicht zurück zu den Grundsätzen der mechanistischen Lehre Newtons. Eine wirkliche Lösung erfordert sowohl die Korrektur der EINSTEINschen als auch der NEWTON’schen Lehre. Aus ihren Bausteinen läßt sich eine neue, zeitgemäße Physik erschaffen.“

c) Der zukunftsweisende Beitrag von Frank D. MARTIN

Der Tagungsband enthält insgesamt 45 wissenschaftliche Beiträge von Autoren aus Deutschland, Österreich, Schweiz, Großbritannien, Griechenland, USA, UdSSR und CSSR. Darunter befassen sich 11 Beiträge speziell mit der Problematik der NEWTON’schen Gravitationstheorie. Unter den letztgenannten ist besonders die Arbeit von Frank D. MARTIN bemerkenswert. MARTIN schreibt (Zitat von Seite 114 des Tagungsbandes):

„Newton machte aus der natürlichen Kreisbewegung einer schwerelosen, z. B. um die Erde kreisenden Masse eine „ursächlich“ gerade Bewegung, die erst durch eine beschleunigende „Anziehungskraft“ der Erde in eine gekrümmte Umlaufbahn fallen sollte!“

Anfangs hielten wir diese Aussage für blanken Unsinn, denn es gilt doch als hinlänglich theoretisch und experimentell nachgewiesen, daß ein kräftefreier, schwereloser Körper entweder ruht oder linear-gleichförmig bewegt ist. Außerdem ist MARTINs Behauptung einer natürlichen Kreisbewegung insofern unvollständig, als sie vollkommen undefiniert läßt, ob die Krümmung der Kreisbewegung – aus der Sicht eines Beobachters – nach rechts, nach links, nach oben, nach unten oder sonst wie verläuft. Es bleibt somit auch offen, ob die natürliche Kreisbewegung beispielsweise um die Erde, den Mond, die Sonne oder überhaupt keinen Himmelskörper orientiert ist. Ohne das Vorliegen einer Ursache dieser Orientierung scheint somit die lineare Bewegung entsprechend NEWTONs Axiom zwingend zu sein.

d) Weiterbildung der Gedanken von Frank D. MARTIN

Angeregt durch die Aussagen von MARTIN und motiviert durch die weiteren kritischen Arbeiten im Tagungsband von 1988 führten wir eigene Recherchen durch. Dabei fiel uns die Arbeit FAHR / KNAPP (1989) in die Hände. Der Untertitel dieser Arbeit ist erstaunlich lang und lautet (Zitat):

„Was ist mit den Galaxien los? Sie drehen sich in ihren Randbereichen viel schneller, als es die Gesetze der Physik erlauben. Oder stimmt etwas nicht mit diesen ehrwürdigen Gesetzen? Der englische Physiker Sir Isaac Newton hatte vor 300 Jahren das Gravitationsgesetz aufgestellt – ein Grundgesetz für die Berechnung der Bewegungen in unserer Welt. Die Galaxien haben das Gesetz nun ins Wanken gebracht. Die Astronomen und Physiker stehen vor dem Dilemma, zwischen den beiden Alternativen entscheiden zu müssen: Täuschen uns die Himmels- Beobachtungen eine andere Welt vor – oder rechnen wir seit Jahrhunderten falsch?“

Im Mai 1994 wurden wir auf das Buch WALKER (1990): „Ein Ball mit Drall – Unterhaltsame Experimente aus Spektrum der Wissenschaft“ aufmerksam gemacht. In diesem Buch werden u. a. Spielzeugkreisel, Bumerangs, Racquetball, Squash, Billard, Achterbahnen und Kirmeskarussells behandelt. Hierdurch angeregt entstanden die Fragen: Sollte NEWTON vielleicht den Einfluß der Rotation der Himmelskörper außer acht gelassen haben? Gab es überhaupt zu Newtons Zeiten hinreichende Kenntnisse zum Drall (Drehimpuls) und zu den Kreiselgesetzen?

Eine erste mathematische Behandlung brachte das Ergebnis, daß aufgrund des sog. Superpositionsprinzips die Bewegung von Himmelskörpern ausschließlich von der Schwerpunktsbewegung, nicht jedoch vom überlagerten Drehimpuls abhängig sei. Aber jetzt ergab sich die Frage: Ist das Superpositionsprinzip überhaupt jemals experimentell überprüft worden? Ist es vielleicht nur eingeführt worden, weil man an die Richtigkeit der NEWTON’schen Axiomatik glaubte? Ist es vielleicht lediglich ein ungeprüftes mathematisches Axiom oder gar ein wissenschaftliches DOGMA?

Weitere Recherchen führten zu dem Ergebnis: Das Superpositionsprinzip ist für diesen Anwendungsfall nie experimentell überprüft worden. Es ist auch aus mathematischen Gründen hier nicht anwendbar, da die Rotation (Drall, Drehimpuls) ein nichtlinearer Vorgang ist.

In dem bei WALKER (1990) zitierten Buch von MAGNUS (1965) heißt es (Zitat von Seite 11, Mitte).

„Neben seinen Drehbewegungen kann ein Kreisel auch Fortschreitbewegungen ausführen, bei denen er sich längs irgendeiner Bahn im Raum fortbewegt – man denke zum Beispiel an die Taumelbewegungen eines rotierend geworfenen Diskus. Die Physik lehrt nun, daß die Drehbewegungen um den Schwerpunkt eines Körpers von den Fortschreitbewegungen getrennt untersucht werden können.“

Merkwürdigerweise sagt MAGNUS in diesem Buch nichts darüber aus, ob und wodurch die Feststellung: „Die Physik lehrt nun . . .“ theoretisch fundiert ist, obwohl seine übrigen Ausführungen eine große theoretische Präzision erkennen lassen.

In dem späteren Buch MAGNUS / MÜLLER (1987) heißt es auf S. 216, letzter Absatz, bis S. 217, erster Abs. (Zitat):

„Bei vielen Bewegungen . . . . darf man sich die Gesamtmasse eines Systems im Massenmittelpunkt konzentriert vorstellen („Punktmasse“) und kann dessen Bewegungen mit Hilfe des Impulssatzes (6.14) oder des Schwerpunktsatzes (6.15) berechnen. In allgemeinen Fällen müssen jedoch Impulssatz und Drallsatz gemeinsam verwendet werden, da die Dehbewegungen dann mit den Bahnbewegungen des Massenmittel-punktes verkoppelt sind.“

Diese Aussage führt bei Anwendung der Kreiselgesetze auf Himmelskörper zu der Erkenntnis:

Maßgebend für die Bewegungsbahn von sich drehenden Himmelskörpern, die frei von äußeren Kräften sind, ist sowohl der Anfangs-Impuls als auch der Anfangs-Drehimpuls (beides sind Vektoren!). Eine Geradlinigkeit dieser Bahn ist im allgemeinen nicht gegeben. (Ausnahme: Drehachse zeigt in Richtung der Schwerpunktsbewegung, Prinzip des Dralles bei Artilleriegeschossen). Die Kreis- und Ellipsenbahnen von Planeten und Mond benötigen keine Fernkräfte, die – ggf. mittels eines sogenannten „Äthers“ – über kosmische Entfernungen übertragen werden. Attraktionskräfte (gemäß heute gängiger Lehrbuch-Darstellungen) nach dem NEWTON’schen Gravitationsgesetz

F	=    G · (M · m) / r²
mit    F	=    Attraktionskraft
G	=    Gravitationskonstante
M    und    m	=    beteiligte Massen eines Zweikörpersystems
r	=    Abstand der Schwerpunkte der Massen M und m

erweisen sich als Fiktionen, die mit der Realität unvereinbar sind. Die krummlinigen Bahnen von Himmelskörpern sind daher weder abhängig von der Größe einer zentralen Masse M noch abhängig von dem Abstand r der beteiligten Massen. Eine zentrale Masse – zentrisch oder exzentrisch – kann also vorhanden sein, sie kann aber auch fehlen.

Newton selbst schrieb (Zitat aus SZTATECSNY 1968, S. 2 unten bis S. 3):

„Es ist tatsächlich unbegreiflich, wie unbeseelte, unvernünftige Materie ohne die Vermittlung von irgend etwas anderem, welches nicht materiell ist, auf andere Materie wirken und auf dieselbe ohne gegenseitige Berührung wirken könne, wie es geschehen müßte, wenn die Gravitation in dem Sinne von Epikur der Materie wesentlich und inhärent und anerschaffen sein sollte, so daß ein Körper auf einen anderen wirken könnte, auf die Entfernung hin durch den leeren Raum, ohne die Vermittlung von irgend etwas, durch welches ihre Aktion und ihre Kraft von einem zum andern geleitet werden könnte, das ist nach meinem Dafürhalten eine so große Absurdität, daß ich glaube, kein Mensch, welcher in philosophischen Dingen eine genügende Denkfähigkeit hat, jemals darauf verfallen kann.“

Diese kritischen Äußerungen NEWTONs beruhen auf der Tatsache, daß er sich selbst im wesentlichen nur für den mathematischen Teil seiner Untersuchungen verantwortlich fühlte. Denn die physikalischen Hypothesen dazu, vor allem die Hypothese einer allgemeinen, von 1/r² abhängigen Gravitationskraft, hatte ihm der in London lebende Physiker Robert Hooke geliefert. Hooke hatte während seiner Tätigkeit als Sekretär der Royal Society von 1677 bis 1681 verschiedene Leute, u. a. auch Newton, für seine Vorstellung von einer allgemeinen Gravitationskraft zu interessieren versucht. Newton nahm die in der Anregung von Hooke enthaltene mathematische Herausforderung an. Er war offenbar der einzige im Kreis der an mathematischen, astronomischen und physikalischen Fragen interessierten Mitglieder der Royal Society, der dieser Aufgabe gewachsen war (vgl. hierzu SCHNEIDER 1987, S. 96, letzter Abs., bis S. 97, erster Abs., und IHMIG 1989, S.27, Mitte).

Der Grund dafür, daß diese kritischen Äußerungen Newtons viele Jahre unbeachtet blieben, liegt darin, daß Newtons „Principia mathematica philosophiae naturalis“ von 1687 von begeisterten Anhängern Newtons, vor allem von VOLTAIRE, uminterpretiert und so auf dem europäischen Festland popularisiert wurden. Dies geht sehr klar aus einer Studie von BORZESZKOWSKI und WAHSNER (1980) hervor. Dort heißt es (Zitat von S. 5):

„Durch den Vergleich NEWTONscher und VOLTAIREscher Schriften wird belegt, daß VOLTAIRES Popularisierung der klassischen Mechanik zugleich aber auch eine Uminterpretation war, die der Zeit entsprach und das Weltbild entscheidend prägte. Da die Mechanik in dieser, ihren physikalischen Inhalt inadäquat rezipierenden, philosophischen Auslegung verbreitet wurde, entstand die Meinung, sie sei mechanistisch.“

Die Ursache der fast 300 Jahre alten Fehlinterpretationen liegt begründet in NEWTONs 1. Axiom: „Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.“ Dieses Axiom wurde damals als bewiesenes Naturgesetz betrachtet und in die mathematischen Ansätze NEWTONs als Prämisse eingeführt. Man erkannte noch nicht, daß es sich um ein Axiom im Sinne einer rein definitorischen Festsetzung handelte. Denn es hatte sich bei Experimenten auf der (kugelförmigen) Erde – im Rahmen der damaligen Meßgenauigkeiten – vielfach bewährt. Dieses 1. Axiom stellt jedoch eine einschränkende Axiomatik dar, die nur auf Körper ohne Drehimpuls anwendbar ist.

Ersetzt man jedoch in NEWTONs 1. Axiom den Begriff „Körper“ durch „Körper ohne Drehimpuls“, so löst sich das angesprochene Problem. Denn nun wird ein bewegter Körper mit Drehimpuls durch mindestens zwei gleiche, mit Abstand starr miteinander verbundene Punktmassen P und Q darstellbar, die um den gedachten (fiktiven) Schwerpunkt S rotieren (siehe BILD, die geradlinigen Pfeile deuten Geschwindigkeitsvektoren zum Zeitpunkt t = 0 an, der krummlinige, ausgezogene Pfeil kennzeichnet den Drehsinn).

Punktmassen besitzen definitionsgemäß unendlich kleine Abmessungen und haben daher jeweils für sich den Drehimpuls NULL. Bei Anwendung von NEWTONs 1. Axiom auf beide Punktmassen ergeben sich über die starre Verbindung von P und Q Trägheitskräfte, die eine geradlinige Bewegung des Schwerpunktes S verhindern. Es folgt eine Bewegungsbahn von S entsprechend dem krummlinigen, punktierten Pfeil im BILD (Computer-Simulation).

NEWTON ging außerdem von der Hypothese aus, daß die „gravitiven“ Kräfte im Kosmos und auf der Erdoberfläche den gleichen physikalischen Ursprung haben. Diese Hypothese können wir weiterhin aufrecht erhalten. Denn unter der oben begründeten Voraussetzung, daß ein kräftefreier Körper im allgemeinen eine krummlinige Bewegungsbahn durchläuft, ergibt sich das irdische Fallen nahezu von selbst, wie Frank D. MARTIN in seinem Buch von 1986: „Die Seele des Kosmos“ zutreffend zum Ausdruck bringt (Zitat von Seite 71, Abs. 2):

„So ist eine bestimmte Mindestgeschwindigkeit erforderlich, um eine Umlaufbahn zu erreichen – ein Fallen zu verhindern -, und eine bestimmte Höchstgeschwindigkeit darf nicht überschritten werden, um ein Entweichen zu vermeiden. Was zählt, ist also die Geschwindigkeit, und keine irgendwie geartete Beschleunigung!“

Unter diesem Aspekt wird auch die „Äquivalenz“ von träger und schwerer Masse zu einer logischen Notwendigkeit. Lediglich die Ursache der krummlinigen Bewegungsbahn hat MARTIN noch nicht richtig erkannt. Diese liegt eindeutig im Drehimpuls begründet, der durch seinen Betrag und seine vektorielle Richtung die jeweilige Krümmung und die Orientierung (vgl. Bemerkung am Schluß des Abschnittes c) der vorliegenden Arbeit) der krummlinigen Bewegunsbahn bestimmt.

Auf der Erdoberfläche wird ein anderer, wesentlicher Aspekt des Drehimpulses deutlich: Für einen auf der Erdoberfläche „ruhenden“, d. h. mit der Erdrotation mitbewegten Beobachter erscheint ein auf der Erdoberfläche„ ruhender“ Körper ohne Rotation, also ohne Drehimpuls. Aus kosmischer Sicht jedoch ist sowohl der Beobachter als auch der betrachtete Körper mit der Erde im 24-Stunden- und Jahres-Rythmus rotierend. Die Rotation eines Körpers ist also – ebenso wie eine lineare Bewegung – eine relative, vom Beobachter abhängige Größe (kognitives Problem). Trägheitskräfte dagegen sind real vorhanden. Beispielsweise fliegt eine zu schnell rotierende Maschine auseinander und zerstört sich selbst, unabhängig davon, wo sich ein Beobachter gegebenenfalls befindet. – Die Untersuchungen zur Realisierung der genannten Hypothese für die Erdoberfläche sind derzeit noch nicht abgeschlossen.

e) Der Glaube an die Weltmaschine

Hier könnte nun der Einwand erhoben werden, die vorstehend entwickelte Auffassung sei unmöglich richtig, da eine Vorausberechnung der Bewegungen der Planeten und anderer Himmelskörper nicht möglich sei. Dies ist aber – entgegen einer weitverbreiteten Meinung – schon mit den überlieferten Gleichungen nicht möglich, da ohne empirisch ermittelte Anfangsbedingungen (Anfangs-Position und Anfangs-Geschwindigkeitsvektor des jeweiligen Himmelskörpers) keine der Bewegungsbahnen berechnet werden kann. Lediglich die Charakteristik einer Kreis- oder Ellipsenbahn (KEPLER-Ellipse) läßt sich im Rahmen eines Zweikörperproblems mit NEWTONs Gleichungen darstellen. Diese Bahn wird jedoch – im Widerspruch zu den Erkenntnissen von KEPLER – bereits bei einem Mehrkörperproblem verfälscht durch die NEWTON zugeschriebene Annahme, daß alle Planeten wechselweise gegeneinander gravitieren sollen. Ferner ist zu berücksichtigen, worauf z. B. HAWKING hinweist (HAWKING 1988, Zitat von S. 212, Mitte):

„Wir können noch nicht einmal exakte Lösungen für die Bewegung dreier Körper in Newtons Gravitationstheorie finden, und die Schwierigkeiten wachsen mit der Zahl der Körper und der Komplexität der Theorie.“

Es wurde seinerzeit von vielen Wissenschaftlern – getragen von dem Glauben an die Göttlichkeit der himmlischen Ordnung – irrtümlich dasjenige als naturgesetzlich angesehen, was in Wirklichkeit lediglich ein Erscheinungsbild langer Zeiträume ist. Vorgänge des täglichen Lebens erlebt der Mensch schon nach kurzer Zeit als nicht konstant ablaufend, weshalb eine kausale Abhängigkeit von äußeren Einflüssen gesucht und formuliert wird. Bewegungsabläufe jedoch, die mehrere Menschenleben scheinbar gleichartig überdauern, werden verständlicherweise als unveränderlich und daher einem höheren Gesetz unterworfen angesehen.

Schon wiederholt ist der „Glaube an die Weltmaschine“ als verfehlte Wissenschaftsauffassung herausgestellt worden, vergleiche z. B. DINGLER (1932), THÜRING (1967), TETENS (1984), FAHR (1992).

THÜRING (1967) schreibt (Zitat von S. 250, 2. Abs.):

„Wenn das axiomatische und somit nicht ontologische, sondern methodologische Wesen der Geometrie, der Kinematik und Mechanik, insbesondere der Gravitation und der Kausalität einmal allen geistigen Menschen bewußt geworden sein wird, wenn man eingesehen haben wird, daß das alles keine „Naturgesetze“ sind, sondern u. a. den Charakter von Herstellungsanweisungen für den Bau von Meßgeräten oder für die Realisierung bestimmter Grundformen und Ungestörtheiten hat, wenn es allen einmal bewußt geworden sein wird, daß das „Kausalitäts-Gesetz“ weder im Atomaren noch im Makroskopischen (Astronomischen) eine ontologische, d.h. von unserem Willen unabhängige Existenz besitzt, dann wird der Gedanke, das Weltall werde von ewigen und allgemeinen, ihm innewohnenden Gesetzen beherrscht und gelenkt – mag dieser Gedanke zunächst noch so erhaben erscheinen – auf die Liste der großen Menschheits-Irrtümer geschrieben und das Gespenst der Großen Weltmaschine wird restlos zerstört sein. Freilich, Vorurteile – und der Empirismus ist ein solches – haben ein zähes Leben. Wer jedoch die alte Maschinen-Auffassung der Welt überwunden haben wird, der wird auch von der Gefahr befreit sein, sich selbst und seine Mitmenschen als Automaten betrachten zu müssen.“

Durch die vorstehend begründete Beschreibung der kosmischen Bewegungen mittels Impuls und Drehimpuls zusammen mit der Widerlegung der MAXWELL’schen Elektrodynamik (FRIEBE 1994, 1995) wird der Begriff der absoluten Ruhe (beispielsweise: absoluter Raum, physikalischer Raum, Ätherhypothese, Neutrinomeer, Tachyonenfeld, Quantenvakuum) überflüssig. Das Relativitätsprinzip der klassischen Mechanik ist zwanglos anwendbar, wie es EINSTEIN ursprünglich vermutet hatte (Zitat EINSTEIN 1905, S. 891, Abs. 2):

„Beispiele ähnlicher Art, sowie die mißlungenen Versuche, eine Bewegung der Erde relativ zum „Lichtmedium“ zu konstatieren, führen zu der Vermutung, daß dem Begriffe der absoluten Ruhe nicht nur in der Mechanik, sondern auch in der Elektrodynamik keine Eigenschaften der Erscheinungen entsprechen, sondern daß vielmehr für alle Koordinatensysteme, für welche die mechanischen Gleichungen gelten, auch die gleichen elektro-dynamischen und optischen Gesetze gelten, wie dies für die Größen erster Ordnung bereits erwiesen ist. Wir wollen diese Vermutung (deren Inhalt im folgenden „Prinzip der Relativität“ genannt werden wird) zur Voraussetzung erheben . . . . “

Literatur

---

• Homepage

FRIEBE, E. (1995): „Die Vektorprodukte der MAXWELL’schen Elektrodynamik“,
DPG-Didaktik-Tagungsband 1995, S. 394 – 399.
Hrsg.: Deutsche Physikalische Gesellschaft (Überarbeitete Fassung vom 9. Oktober 2002).

a) Zusammenfassung

Die MAXWELL’sche Elektrodynamik wird in der Regel in Form von Differentialgleichungen geschrieben. Diese haben ihren Ursprung in Vektorprodukten, aus denen durch Differentiation (Rotor-Operation) die homogenen Gleichungen der MAXWELL’schen Elektrodynamik ohne zusätzliche Annahmen direkt ableitbar sind. Das Vektorprodukt ist aus der klassischen Mechanik bekannt und dient dort vor allem zur Beschreibung des Drehmomentes, das sich aus dem Kraft-Vektor und dem Kraftarm-Vektor ableitet. Aus Dimensionsgründen gilt aber die Bedingung, daß der dem Vektorprodukt zugeordnete Vektor nicht mit einem normalen Vektor vektoriell addiert, subtrahiert oder multipliziert werden darf. Bei der MAXWELL’schen Elektrodynamik wird gegen diese Bedingung verstoßen. Daraus ergeben sich Fehlaussagen, die für die Probleme der speziellen Relativitätstheorie mit verantwortlich sind. Vor allem läßt sich aus der MAXWELL’schen Elektrodynamik eine Aussage über die Lichtgeschwindigkeit (angebliche absolute Konstanz) nicht ableiten.

b) Die Gleichungen der MAXWELL’schen Elektrodynamik

Die Elektrodynamik von MAXWELL (1865) ist seit ihrer ersten Formulierung vielfach verändert worden. Ihre Kernaussage ist aber stets die gleiche geblieben und findet ihren Ausdruck in den folgenden Gleichungen. Man nennt sie auch die homogenen Gleichungen der MAXWELL’schen Elektrodynamik:

Dabei sind gemäß Voraussetzung

von Ort und Zeit unabhängige Konstanten. Der Operator   rot    in den vorstehenden Gleichungen stellt in bekannter Weise eine spezielle Differentiation nach drei Raumkoordinaten dar. Bei Zusammenführung beider Gleichungen (1) und (2) – unter Anwendung der sogenannten Wellen- gleichung – ergibt sich als Wellengeschwindigkeit:

Diese Wellengeschwindigkeit   c    wird in der Regel als „Vakuum-Lichtgeschwindigkeit“ bezeichnet. Da die Größen

üblicherweise als Naturkonstanten des Vakuums interpretiert werden, ist daraus eine absolute Konstanz der Vakuum-Lichtgeschwindigkeit gefolgert worden. Diese Folgerung galt viele Jahre als experimentell bestens bestätigt und war dadurch zu einem wissenschaftlichen Dogma erstarrt. Durch die umfangreichen Untersuchungen von KANTOR (1976) (siehe auch: FRIEBE, E. 1992) ist aufgezeigt worden, daß die Lichtgeschwindigkeit in Wirklichkeit von der Bewegung ihrer Quelle zum Zeitpunkt der Emission von der bewegten Quelle abhängt. Es sind daher auch Überlichtgeschwindigkeiten zwanglos möglich (vgl. KANTOR 1976, Seite ’v’: ’PREFACE’, siehe auch: FRIEBE, E. 1992).

Die Gleichungen (1) und (2) sind zunächst nicht auf „bewegte Systeme“ anwendbar, d. h. auf solche Systeme, bei denen Lichtquelle und Lichtempfänger (Sendeantenne und Empfangsantenne) relativ zueinander bewegt sind. Eine mathematische „Transformation“ auf bewegte Systeme ist bisher mit den sogenannten Lorentztransformationen versucht worden, die wesentlicher Bestandteil der speziellen Relativitätstheorie sind. Diese führten aber zu zahlreichen Widersprüchen („Paradoxa“), wie die öffentliche Diskussion der speziellen Relativitätstheorie gezeigt hat (vgl. FRIEBE, E. 1992). Im folgenden soll nun die Ursache dieser Widersprüche aufgezeigt werden.

c) Die der MAXWELL’schen Elektrodynamik zugrundeliegenden Vektorprodukte

Unabhängig davon, wie MAXWELL seinerzeit zu seinen Gleichungen gekommen ist, müssen wir uns vor Augen halten, worin diese ihren eigentlichen Ursprung haben. In anderem Zusammenhang hat POHL (1967, S. 80/81 und S. 142/143) wesentlich einfachere Gleichungen zur Elektrodynamik angegeben, welche als Vektorprodukte formuliert sind. Sie lauten:

In diesen Gleichungen stellt   ×  den Operator für das jeweilige Vektorprodukt und u zunächst den Vektor einer beliebigen Geschwindigkeit dar, die prinzipiell sowohl kleiner als auch größer als die bekannte Vakuum-Lichtgeschwindigkeit sein kann. Für den Fall der Ausbreitung elektromagnetischer „Wellen“ ist u gleich der Vakuum-Lichtgeschwindigkeit c, deren Betrag sich nach POHL 1967, S. 142, aus seiner Gleichung (154) errechnet, die mit der oben genannten Gleichung (3) identisch ist. Wesentlich ist, daß in den Gleichungen (80) und (83) – im Gegensatz zu den Gleichungen (1) und (2) – die Vakuum-Lichtgeschwindigkeit als ein echter, dreidimensionaler Vektor auftritt.

Die Gleichungen (80) und (83) von POHL (1967) stellen die eigentliche Grundlage der MAXWELL’schen Theorie deshalb dar, weil aus ihnen durch Differentiation (Rotor-Operation) die Gleichungen (1) und (2) ohne zusätzliche Annahmen direkt ableitbar sind. Dabei folgt Glg. (1) aus Glg. (80) und Glg. (2) aus Glg. (83). (siehe: FRIEBE, E. 2002)

In der MAXWELL’schen Theorie wird – gemäß Lehrbuch – die Lichtgeschwindigkeit c [vgl. Glg. (3)] durch Verknüpfung der Gleichungen (80) und (83) – über den Umweg der davon ableitbaren Gleichungen (1) und (2) – errechnet. Keine der Gleichungen (80), (83), [oder (1) und (2)] ist für sich zur Berechnung von  c hinreichend. Denn keine dieser vier Gleichungen enthält beide Konstanten

Gemäß Glg. (80) ist aber der Vektor H ein Vektorprodukt, das – wie nachstehend anhand des Drehmomentes der klassischen Mechanik näher erläutert wird – nicht mit einem normalen Vektor vektoriell multipliziert werden darf. Der Vektor H aus Glg. (80) darf also nicht mit der Glg. (83) verknüpft werden. Das gleiche gilt für den Vektor E der Gleichung (83), der ebenfalls ein Vektorprodukt darstellt und daher nicht mit Glg. (80) mathematisch verknüpft werden darf. Die Lichtgeschwindigkeit c kann also aus den Gleichungen (80) und (83) [oder (1) und (2)] – entgegen zahlreichen Lehrbuchdarstellungen – nicht abgeleitet werden. Dies soll im folgenden gezeigt werden.

d) Das Drehmoment der klassischen Mechanik

In der klassischen Mechanik wird neben dem Begriff Kraft, der zur Darstellung linear gerichteter Wirkungen dient, auch der Begriff Drehmoment zur Darstellung von drehend angreifenden Wirkungen verwendet. Das Drehmoment kann auch als die Wirkung eines Kräftepaares zweier entgegengerichteter, gleichgroßer, paralleler Kräfte beschrieben werden. Für eine mathematische Behandlung wird das Drehmoment in der Regel als Vektorprodukt in folgender Weise formuliert:

Der Vektor (M ) des Vektorproduktes steht gemäß Definition senkrecht auf der Ebene der beiden anderen Vektoren (a und F). Sein Richtungssinn ist durch die sogenannte Schraubenregel festgelegt. Diese Schraubenregel wird durch BILD 1 veranschaulicht, das dem Buch entnommen ist:

„Physik – Ein Lehrbuch“ von Wilhelm H. Westphal,
13. Auflage (1948), Seite 18, Abb. 14.

Aus der Gegenüberstellung der Skizzen a) und b) von BILD 1 ist ersichtlich, daß sich – abhängig von der Reihenfolge der Faktoren des Vektorproduktes – der Richtungssinn des Vektors des Vektorproduktes umkehrt. Diese Darstellung als Vektor und dessen Richtungssinn ist eine reine Konvention und wird durch eine rechtsgängige Schraube – als eine Art Eselsbrücke – plausibel gemacht. Diese Festlegung bietet die Möglichkeit, daß mehrere Vektorprodukte (z. B. Drehmomente) wie normale Vektoren (z. B. Kräfte) vektoriell addiert und subtrahiert (nicht jedoch multipliziert) werden können. Wegen des qualitativen Unterschiedes eines drehend angreifenden Drehmomentes (Dimension: [kp m]) gegenüber einer linear gerichteten Kraft (Dimension: [kp]) gilt aber die Bedingung, daß der Vektor eines Drehmomentes nicht mit dem Vektor einer Kraft vektoriell addiert, subtrahiert oder multipliziert werden darf.

Diese bei der klassischen Mechanik ohne weiteres aus der reinen Anschauung heraus einsichtige Bedingung gilt aus Dimensionsgründen auch allgemein für Vektorprodukte. Bei mathematischen Ableitungen, bei denen aus der Anschauung heraus eine Überprüfung nicht üblich oder nicht möglich ist, ist daher die Beachtung dieser Bedingung besonders wichtig. In der MAXWELL’schen Elektrodynamik jedoch ist diese Bedingung außer acht gelassen worden. Hierbei wird nämlich sowohl das Formelsymbol E als auch das Formelsymbol H  wechselweise einem normalen Vektor und einem Vektorprodukt zugeordnet. Dies verletzt die zu fordernde Identität und ist aus Dimensionsgründen unzulässig. Der dadurch bedingte Fehler kann auch nicht durch Multiplikation mit einem Skalar

bereinigt werden. Deshalb ist die MAXWELL’sche Theorie in wesentlichen Teilen fehlerhaft [vgl. auch CATT (1980)].

e) Experimentelle Bestätigungen der Elektrodynamik

Es könnte nun der Einwand erhoben werden, daß sich die MAXWELL’sche Elektrodynamik in der Praxis hervorragend bewährt habe und weitgehend experimentell bestätigt worden sei. Diese Aussage beruht auf grundlegenden Mißverständnissen.

Ausgangspunkt der MAXWELL’schen Gleichungen waren die experimentellen Untersuchungen von FARADAY. Hierauf nimmt MAXWELL (1865) speziell Bezug. Besondere Bedeutung kommt dabei dem Induktionsgesetz nach FARADAY zu, das bereits vor der Formulierung der MAXWELL’schen Elektrodynamik experimentell bestätigt war und der Theorie als Grundlage diente. Die mathematische Beschreibung des Induktionsgesetzes durch die Glg. (2) hat sich seit vielen Jahrzehnten hervorragend bewährt. Das Induktionsgesetz wird in der Fachliteratur zutreffend und sehr ausführlich behandelt.

Zur Formulierung der Glg. (1) dagegen führte MAXWELL – in Ermangelung experimenteller Ergebnisse – die Hypothese vom Verschiebungsstrom (displacement current) ein.

Dies soll an BILD 2 veranschaulicht werden, das die elektrische Entladung eines Plattenkondensators durch einen zeitlich veränderlichen Strom zeigt. Die MAXWELL’sche Hypothese besagt nun, daß nicht nur der Strom im elektrischen Leiter von magnetischen Feldlinien (H,  BILD 2 links), sondern daß auch zeitlich veränderliche elektrische Felder

(rechte Seite der Glg. 1) von eben solchen magnetischen Feldlinien umgeben seien (H,  BILD 2 rechts)

Durch die sehr ausführlichen Untersuchungen von CATT (1978, 1979, 1982, 1984, 1985, 2001, 2002) ist inzwischen gezeigt worden, daß diese MAXWELL’sche Hypothese – entgegen einer weitverbreiteten Meinung – nicht der physikalischen Realität entspricht. BILD 3, das aus CATT (1979) – geringfügig abgeändert – entnommen ist, macht dies deutlich. Ein elektromagnetischer Impuls (BILD 3, oben) würde auf einer Übertragungs-Doppelleitung (Lecher-Leitung, BILD 3, unten) sich selbst vorauslaufen, wenn – außer den elektrischen Leitern – auch die E-Feldlinien von H-Feldlinien ringförmig umgeben wären. Überlichtgeschwindigkeiten relativ zur Doppelleitung wären die Folge. (Näheres hierzu siehe CATT 1978, 1979, 1982, 1984, 1985, 2001, 2002). Diese Betrachtung zeigt die Unrichtigkeit der genannten MAXWELL’schen Hypothese.

Im allgemeinen wird behauptet, die MAXWELL’sche Hypothese sei bereits vielfach experimentell bestätigt worden. Diese Aussage beruht auf grundlegenden Irrtümern. Beispielsweise schreibt POHL auf S. 78 seines Lehrbuches von 1967 (Zitat, im Original kein Fettdruck):

„Ein wirklicher Beweis für das Magnetfeld des Verschiebungsstromes kann nur bei Benutzung ringförmig geschlossener elektrischer Feldlinien geführt werden. Er wird erst in Kap. XII erbracht, und zwar durch den Nachweis frei im Raum fortschreitender elektrischer Wellen. Bis dahin bleibt das Magnetfeld des Verschiebungsstromes eine nur plausibel gemachte Behauptung.“

Der sogenannte Nachweis des Verschiebungsstromes in Kap. XII bei POHL (1967), wird auf S. 139, Absatz 2, behandelt. Dort wird auf die Abb. 300 von S. 135 Bezug genommen. Die in Verbindung mit Abb. 300 besprochene Versuchsanordnung jedoch untersucht – im Gegensatz zur soeben zitierten Aussage – nur stehende elektrische Wellen auf einer Lecher-Leitung. Die oben in Verbindung mit BILD 3 besprochene Argumentation von CATT (1979) bezieht sich zwar ebenfalls auf eine Lecher-Leitung, nimmt aber auf einen fortschreitenden elektromagnetischen Impuls Bezug. Erst dadurch wird die Unrichtigkeit der MAXWELL’schen Hypothese erkennbar. Um Mißverständnisse zu vermeiden, muß jedoch darauf hingewiesen werden, daß durch die Untersuchungen von CATT lediglich der angebliche Beweis für das Magnetfeld des Verschiebungsstromes widerlegt wird (vgl. hierzu den ersten Satz des vorgenannten Zitats von POHL 1967, S. 78). Der Gedanke einer Fortsetzung eines elektrischen Leiterstromes durch die Feldlinien eines elektrischen Feldes (z. B. in einem Kondensator gemäß BILD 2) bleibt davon unberührt, auch wenn dies nur eine nützliche Hilfsvorstellung bedeutet.

f) Qualitative Betrachtung

Ergänzend zu den Untersuchungen von CATT (1978, 1979, 1982, 1984, 1985, 2001, 2002) soll noch auf rein qualitative Weise gezeigt werden, daß die MAXWELL’sche Elektrodynamik fehlerhaft ist.

BILD 4, das einer Originalarbeit von MAXWELL aus dem Jahre 1861 entnommen ist, läßt erkennen, welche Modellvorstellung der mathematischen Formulierung MAXWELLs ursprünglich zugrunde liegt. Es folgt daraus ein Ausbreitungsverhalten der elektro-magnetischen Erscheinungen, wie es z. B. im Handbuch von THEIMER (1986, Seite 125) veranschaulicht wird (BILD 5).

Dieses Verhalten wurde noch nie beobachtet und weicht auch erheblich von der Darstellung gemäß BILD 6 (nach POHL 1967, S. 141/142) ab, welches das tatsächliche Ausbreitungsverhalten wiedergibt. Hierbei zeigt BILD 6A und 6B die Verteilung des elektrischen, BILD 6C die Verteilung des magnetischen Feldes um einen Dipol.

Der entscheidende Unterschied beider Darstellungen liegt darin, daß gemäß BILD 6 für die magnetischen Feldlinien nur ein axialsymmetrisches Zentrum um den erregenden Dipol vorhanden ist, während gemäß BILD 5 eine unbegrenzte Zahl solcher Zentren unterstellt wird, die als ringförmige magnetische Feldlinien in den Raum hinauswandern. BILD 5 stellt keinen Sonderfall des Ausbreitungsverhaltens nach BILD 6 dar. Auch lassen sich die beiden Bilder nicht ineinander überführen.

Aufgrund der vorstehenden Untersuchungen, die auf den Ergebnissen von CATT (1978, 1979, 1982, 1984, 1985, 2001, 2002) aufbauen, sind daher die Glg. (1) und die ihr entsprechende Glg. (80) ersatzlos zu streichen. Es verbleiben nur noch die Glgn. (2) oder (83). Eine Verknüpfung zweier Gleichungen ist nun nicht mehr möglich und deshalb kann auch jeweils die rechte Seite der Glgn. (2) oder (83) entfallen, so daß nur noch das Induktionsgesetz in folgender Formulierung verbleibt:

g) Alternativer mathematischer Ansatz zur „Wellenausbreitung“

Schon WALTER RITZ (1878 bis 1909) (siehe RITZ 1908d) hat auf die Entbehrlichkeit der partiellen Differentialgleichungen nach MAXWELL hingewiesen. Er schreibt (Zitat nach RITZ, Übersetzung von DÜRR 1991, S. 8/9, siehe auch RITZ 1908d):

„Die Theorie läßt unendlich viele Lösungen zu, die alle den gesetzten Bedingungen entsprechen, aber der Erfahrung widersprechen und z. B. zu einem perpetuum mobile führen. Um solche Lösungen auszuschließen, muß man im Sinn einer Hypothese die Formeln der retardierten Potentiale einführen. Diese bringen die Unumkehrbarkeit der Erscheinungen in die Elektrodynamik, während die allgemeinen Gleichungen mit der Umkehrbarkeit verknüpft sind. Ich werde zeigen, daß sie, im Gegensatz zur überkommenen Meinung, nicht aus einer passenden Spezialisierung des Anfangszustandes ableitbar sind. Sie bedeuten eine neue Hypothese, und diese macht die partiellen Differentialgleichungen überflüssig.“

Wie würde nun ein alternatives mathematischer Konzept zur Beschreibung des Ausbreitungsverhaltens elektromagnetischer Erscheinungen aussehen? Man braucht hierzu lediglich auf einen bekannten Ansatz zurückzugreifen, nämlich auf die „Wellengleichung“ in integraler Form. Diese lautet:

Diese Gleichung gibt die Amplitude für eine fortschreitende eindimensionale „ Welle“ längs eines linearen Gebildes nach Ort und Zeit wieder. Sie gilt auch für eine zwei- oder dreidimensionale „Welle“ in Richtung x . Diese Abhängigkeit in ihrer dreidimensionalen, differentiellen Form hat RITZ als die Formeln der retardierten Potentiale bezeichnet. Um die Glg. (5) zu formulieren, bedarf es der MAXWELL’schen Gleichungen nicht. Letztere sind also nicht nur fehlerhaft sondern auch zur Beschreibung des Ausbreitungsverhaltens elektromagnetischer „Wellen“ entbehrlich.

Die Glg. (5) ist andererseits nicht an einen absoluten Raum bzw. ein Lichtmedium (Äther) gebunden. Sie kann daher auch zur Aufstellung einer ballistischen Theorie dienen, die eine konstante Ausbreitungsgeschwindigkeit einer elektromagnetischen „Welle“ relativ zur emittierenden Quelle voraussetzt, wie es WALTER RITZ schon in den Jahren 1908/1909 (vgl. Übersetzung aus 1991, siehe auch RITZ 1908d) gefordert hat. In der Arbeit: „Ballistische Modellvorstellung zur Elektrodynamik und Optik“ (FRIEBE, E. 1993) wird gezeigt, daß mit einer einfachen ballistischen Modellvorstellung, bei der die „elektrischen Kraftlinien“ nach FARADAY als materielle, korpuskular aufgebaute Ketten von Elementarteilchen beschrieben werden, alle wesentlichen elektromagnetischen Erscheinungen auf rein klassische Weise erklärt werden können.

Literatur

---

Homepage

FRIEBE, Ekkehard (1982): „Hertz’sche Wellen“,
Zeitschrift „Wissen im Werden“, Zwingendorf (Österreich), Heft 2 (1982), S. 81 – 86 

Im Jahre 1889 brachte Heinrich HERTZ seine viel zitierte Arbeit heraus: „Die Kräfte elektrischer Schwingungen, behandelt nach der MAXWELL’schen Theorie“. Gleich am Anfang dieser Arbeit führte er aus: „Die Ergebnisse der Versuche, welche ich über schnelle elektrische Schwingungen angestellt habe, scheinen mir der MAXWELL’schen Theorie ein Übergewicht über die anderen Theorien der Elektrodynamik zu verleihen.“ HERTZ geht in dieser Untersuchung von Gleichungen aus, die zwar auf den Grundannahmen von MAXWELL beruhen, die aber teilweise vereinfacht und gestrafft waren. Diese Gleichungen hatte HERTZ in früheren Veröffentlichungen herausgearbeitet. Sie entsprachen denen von HEAVISIDE und haben – in der heute üblichen Darstellungsweise – folgende Form:

dH/dt = – c · rot E                 (1)

dE/dt =   c · rot H                 (2)

div H = 0                              (3)

div E = 0                              (4)

Dabei ist c die Vakuumlichtgeschwindigkeit, H der Vektor der „magnetischen Kraft“ und E der Vektor der „elektrischen Kraft“.

HERTZ zeigt, daß die Ausbreitung der elektromagnetischen Erscheinungen in der Tat – wie es MAXWELL aufgrund von Anregungen durch Faraday vorausgesetzt hatte – etwa mit Vakuumlichtgeschwindigkeit fortschreiten. Seine Untersuchungen zeigen aber auch, daß zur Erregung dieser Erscheinungen ein Dipol erforderlich ist, also eine mechanische Anordnung, die mindestens zwei diskrete, unterschiedlich polarisierte Ladungspunkte erfordert. Nicht hinreichend ist also eine Punktladung oder ein sogenannter „Kugelstrahler“, der in früheren und auch späteren Theorien als ausreichend angesehen wurde. Vor allem ergibt sich durch die ZWEI Ladungspunkte eine eindeutige Richtung für die Polarisierung der entstehenden elektro­magnetischen Welle, die auf andere Weise nicht verständlich gemacht werden kann. Diese Feststellung ist umso wichtiger, als auch bei optischen Erscheinungen schon lange Zeit vorher der Effekt der Polarisation bekannt war.

Durch die Polarisation ergibt sich, daß die Ausbreitung der elektro­magnetischen Erscheinungen nicht in Form einer Kugelwelle vor sich geht, sondern eine Vorzugsrichtung besitzt, die rotationssymmetrisch um die Achse des Dipols liegt und ihr Maximum in der Richtung senkrecht zum Dipol aufweist. HERTZ bediente sich zur Beschreibung dieser Erscheinung des sog. „Biot-Savart’schen Geset­zes“, das er – in Abweichung zum Ansatz von MAXWELL, der den Begriff des „Vektor­potentials“ eingeführt und angewendet hatte – mit den grundlegenden Differential-Gleichungen MAXWELLs verknüpfte. Dabei verzichtete er bewußt auf die exakte Darstellung der unmittelbaren Umgebung des Dipols, indem er in diesem Bereich den Abstand eines zu betrachtenden Raumpunktes von dem sehr klein angenommenen Dipol gegenüber der Wellenlänge vernachlässigte. Hierdurch ergab die Rechnung für den Nahbereich naturgemäß nur eine Annäherung. Andererseits standen die MAXWELL’schen Gleichungen in der oben angegebenen Form für den Fernbereich in recht guter Übereinstimmung mit den experimentellen Ergebnissen.

 

Den Nahbereich konnte HERTZ durch graphische Darstellungen (BILD links, entnommen aus Annalen der Physik und Chemie N. F. Bd. XXXVI, 1889) sehr gut veranschaulichen, die zur qualitativen Beschreibung die­ses Bereiches auch heute noch bestens geeignet sind.

In einer späteren Arbeit entwic­kelte HERTZ auch eine Theorie zur Elektrodynamik bewegter Körper (1890). Diese befrie­digte jedoch nicht im Hinblick auf die experimentellen Erfah­rungen und wurde daher von der Fachwelt verworfen. Erst in neuerer Zeit findet man sie in wissen­schaft­lichen Werken zur Elektrodynamik wieder erwähnt, vor allem in Lehrbüchern für Techniker (z.B. KÜPF­MÜLLER 1973).

Um so mehr fand die von LORENTZ stammende Arbeit: „Versuch einer Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern“ (1895) und eine spätere Arbeit desselben Autors von 1904 Beachtung, bei denen die „Elektronen­Theorie“ entwickelt und auf die MAXWELL’schen Gleichungen angewandt wurde.

Aufgrund dessen erhalten die MAXWELL’schen Gleichungen die folgende Form:

dH/dt         = – c · rot E                 (1a)

dE/dt + á·v =   c · rot H                 (2a)

div H = 0                                     (3a)

div E = á                                     (4a)

Dabei ist nach LORENTZ die „Volumendichtigkeit“ der Ladung des Elektrons und v der Vektor der Geschwindigkeit eines Punktes des Elektrons.

Diese Gleichungen gehen für die Geschwindigkeit v = 0 nicht in die MAXWELL- HERTZ’schen Gleichungen über, da der Ausdruck (4a) div E = á von dem Ausdruck (4) div E = 0 abweicht. In Worten besagt dieser Unterschied, daß beim HERTZ’schen Ansatz die Summe aller elektrischen Feldlinien, die von einem erregenden Dipol ausgehen, unter Berücksichtigung des Richtungsvorzeichens, in einem abge­schlossenen Raumgebiet stets gleich NULL ist, während nach dem Ansatz von LORENTZ von einem Monopol ausgegangen wird, dessen Feldlinien-Summe in einem abgeschlossenen Raumgebiet ungleich NULL ist. Es wird also hierbei implizite vorausgesetzt, daß die Gegenladung des Elektrons, an der die elektrischen Feldlinien enden, in einem Medium (Äther) bzw. im Unendlichen ihren Sitz hat.

Obwohl dieser Unterschied nur sehr klein zu sein scheint, ist er dennoch von wesentlicher Bedeutung, als nunmehr die „experimentellen Bestätigungen“ von HERTZ auf diesen Ansatz nicht mehr zutreffen. Das bezieht sich vor allem auf die Richtung der elektrischen Feldlinien, die beim HERTZ’schen Ansatz im wesentlichen senkrecht zur Ausbreitungsrichtung (Fortpflanzung mit c), beim LORENTZ’schen Ansatz im wesentlichen parallel zur Ausbreitungsrichtung angenommen wird. Zum anderen bringt der Ansatz von LORENTZ für den Fall v ungleich Null Schwierigkeiten, da eine Geschwin­digkeit (= Abstandsänderung pro Zeiteinheit) gegenüber dem Unendlichen nicht und gegenüber einem Medium nur dann definierbar ist, wenn ein solches als vorhanden angenommen werden und in seiner Bewegung relativ zu materiellen Kör­pern meßtechnisch erfaßt werden kann.

Dieser letztgenannten Problematik kann auch dadurch nicht begegnet werden, daß man das Elektron als um einen Schwer­punkt schwingend oder rotierend annimmt, denn die grund­sätzliche Nichtübereinstimmung mit den Versuchsergebnissen von HERTZ bezüglich der Richtung der Feldlinien wird hier­durch nicht beseitigt.

In der heutigen Literatur findet man im allgemeinen Misch­formen zwischen den HERTZ’schen und den LORENTZ’schen Glei­chungen, die zum Teil noch durch Elemente der ursprüngli­chen Ansätze von MAXWELL selbst verändert sind. Dabei wird in der physikalischen Literatur im allgemeinen die Form nach LORENTZ, in der technischen Literatur die Form nach HERTZ bevorzugt. Dieses dürfte ein wesentlicher Grund dafür sein, daß zwischen Physikern und Elektrotechnikern häufig Mißver­ständnisse bei der Diskussion elektro­magnetischer Erscheinun­gen auftreten. Beide sprechen von den „MAXWELL’schen Glei­chungen“, beide meinen aber etwas anderes. Damit verbunden ist ein anderes Problem: Die in der Technik im Rahmen der für Tech­niker ausreichenden Meßgenauigkeiten festgestellten Übereinstimmungen zwischen Theorie und Experiment werden von den Physikern als experimentelle Bestätigung höchster Genauigkeit ihrer theoretischen Ansätze interpretiert.

Es ergibt sich nun die erstaunliche Tatsache, daß die großen Theorien der modernen Physik, d. h. die Relativitäts-Theorie und die Quanten-Theorie, auf der LORENTZ’schen Form der MAXWELL’schen Gleichungen aufbauen, die selbst mit den experi­mentellen Bestätigungen von HERTZ nicht im Einklang steht, obwohl sie sich auf diese beruft. Auch andere sogenannte experimentelle Beweise der Relativitäts- und Quanten-Theorie sind unschlüssig, soweit sie sich bei ihrer Auswertung auf Formeln stützen, die aus der LORENTZ’schen Theorie abgeleitet sind. Vor allem ist in diesem Zusammenhang die Formel für die „LORENTZKRAFT“ zu nennen. Diese Formel bedarf dringend einer logischen und experimentellen Überprüfung, denn sie dient zur Berechnung der sogenannten „Geschwindigkeitsabhängigkeit der Masse“. Bei dieser Formel tritt ebenfalls die Geschwin­digkeit v des Elektrons auf, die die oben genannten begriffli­chen Schwierigkeiten mit sich bringt.

Es erscheint Zeit, daß die unterschiedlichen Formen der „MAXWELL’schen“ Gleichungen kritisch gegenübergestellt und ihre Prämissen und „experimentellen Bestätigungen“ überprüft werden.

 

---

Literatur

1. FRIEBE, E. (1980): „Die MAXWELL’schen Gleichungen in neuer, besonders einfacher mathematischer Form“. München 1980, Privatdruck

2. FRIEBE, E. (1982): „Elektrodynamik und MAXWELL’sche Gleichungen im Einklang mit dem Relativitätsprinzip von Galilei“. Vortrag am 26.3.82 bei der Deutschen Physikalischen Gesellschaft (DPG), Gießen (Tagungsband).

3. HERTZ, H. (1889): „Die Kräfte elektrischer Schwingungen, behandelt nach der MAXWELL’schen Theorie“. Ann. Phys. u. Chem. 1889, No. 1

4. HERTZ, H. (1890): „Über die Grundgleichungen der Elektrodynamik für bewegte Körper“. Ges. Werke, Bd. II, 2. Aufl. Leipzig 1894, S.256 – 285.

5. KÜPFMÜLLER, K. (1973): „Einführung in die theoretische Elektrotechnik“. 10. Aufl. 1973. Springer-Verlag, insb. Abschnitt 43

6. LORENTZ, H. A. (1895): „Versuch einer Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern“. Auszugsweise in „Das Relativitätsprinzip“ von Lorentz, Einstein, Minkowski, 4. Aufl., Teubner Leipzig Berlin 1922

7. LORENTZ, H. A. (1904): „Elektromagnetische Erscheinungen in einem System, das sich mit beliebiger, die des Lichtes nicht erreichender Geschwindigkeit bewegt“. Deutsch aus dem Englischen in „Das Relativitätsprinzip“ (wie unter 6.)

8. MAXWELL, J. C. (1865): „A Dynamical Theory of the Electromagnetic Field“. Philosophical Transactions. 1865 London, Vol. 155, S. 459 – 512

9. MAXWELL, J. C. (1883): „Lehrbuch der Electricität und des Magnetismus“. Deutsch von Dr. B. Weinstein, Bd. I u II, Springer-Verlag, Berlin

---

Homepage

FRIEBE, Ekkehard (1993): „Ballistische Modellvorstellung zur Elektrodynamik und Optik“,
DPG-Didaktik-Tagungsband 1993, S. 681 – 686. Hrsg.: Deutsche Physikalische Gesellschaft

 

Als besondere Eigenart von elektro-magnetischen Wellen (einschließlich des Lichtes) gilt der sogenannte Dualismus „Teilchen-Welle“. Aber sind denn nicht andere Wellenerscheinungen ebenfalls dualistisch? Wasserwellen bestehen aus periodischen Bewegungen von Wassermolekülen, Schallwellen aus wechselnden Kompressionen von Luftmolekülen. – Aber dennoch ist diese Analogie nicht vollkommen. Schauen wir uns doch einmal eine graphische Darstellung von Heinrich HERTZ an (BILD 1, entnommen aus Ann. d. Phys. u. Chem. N. F. Bd. XXXVI, 1889).

BILD 1

Es werden dort Linien sichtbar, die an die „elektrischen Kraftlinien“ nach FARADAY erinnern. Sollten diese Linien etwa Kettenbildungen von elementaren Teilchen sein, wie es durch KOPPELMANN / HENSEL (1988) (vgl. dort insb. Abb. 5e und 6d) für sogenannte Ketten-Cluster modellmäßig aufgezeigt ist? Ketten-Cluster sind kettenartige Aneinanderreihungen von Ionen, die abwechselnd positive und negative Polarität besitzen.

a) Elektrostatisches Feld

Der vorstehend angedeutete Gedanke ist die Grundlage einer ballistischen Modellvorstellung zur Elektrodynamik und Optik. Sie basiert auf der Annahme, daß ein elektrostatisches „Feld“ aus folgenden „Bausteinen“ besteht: Erstens negative Elementar-Ladungen (Elektronen), die sich z. B. auf einer ersten metallischen Platte eines Platten-Kondensators befinden, zweitens positive Elementar-Ladungen (Positronen), die sich auf der zweiten metallischen Platte desselben Kondensators befinden, und drittens Ketten-Cluster, die dazwischen „ausgespannt“ sind und die die „elektrischen Kraftlinien“ nach FARADAY materiell verkörpern (BILD 2). Denn diese Kraftlinien sind durch metallische Körper begrenzt und reichen nicht – wie es die moderne Feldtheorie unterstellt – einseitig bis ins Unendliche.

Diese Modellvorstellung wurde bereits in einer Arbeit von FRIEBE (1985) veröffentlicht. Wegen näherer Einzelheiten wird auf diese Arbeit verwiesen. Hierin ist u. a. eine Reihe experimenteller Befunde näher behandelt (vgl. ebenda S. 25 – 28), die zu dieser Modellvorstellung geführt haben. Ferner werden hierin wesentliche Mängel der MAXWELL-schen Elektrodynamik aufgezeigt.

In der Arbeit von 1985 wurde noch nicht der Begriff Ketten-Cluster eingeführt, sondern die Bezeichnung Polektronen-Ketten verwendet. Hierbei bedeutet die neu eingeführte Bezeichnung Polektron eine Paarbildung zwischen Elektron und Positron und dient der Unterscheidung gegenüber anderen, in ihrer Bedeutung abweichenden Bezeichnungen für diese Paarbildung. Im vorliegenden Bericht soll die Bezeichnung Polektron beibehalten werden.

Gemäß Modellvorstellung haben Elektron und Positron die gleiche Masse, jedoch unterschiedliches Ladungs-Vorzeichen. Das Polektron besitzt die Summe der Massen der erstgenannten und verhält sich im Nahbereich wie ein elektrostatischer Dipol, im Fernbereich jedoch (nahezu) elektrisch neutral. Die Masse von Elektron, Positron und Polektron ist unabhängig von der Geschwindigkeit.

Die Polektronen-Ketten ruhen beim elektrostatischen „Feld“ relativ zu den Kondensator-Platten oder sonstigen metallischen Trägern der Elektronen und Positronen.

---

BILD 2                                                       BILD 3

b) Elektrischer Strom

Eine elektrische Doppelleitung, beispw. bestehend aus zwei parallelen Kupferleitern, ist mit dem Platten-Kondensator verwandt, nur daß die räumliche Ausdehnung wesentlich größer ist und daß z. B. eine Gleichspannungs-Quelle einseitig angeschlossen ist (BILD 3). Auf dem einen Leiter bewegen sich Elektronen, auf dem anderen Leiter Positronen mit Lichtgeschwindigkeit relativ zum Leiter, sofern die Doppelleitung im Vakuum verlegt ist (RÜDENBERG 1962). Zwischen den Leitern bewegen sich die Polektronen-Ketten in gleicher Richtung und mit gleicher Geschwindigkeit.

Zur Beschreibung eines elektrischen Stromes nach der Modellvorstellung sind also dieselben elementaren „Bausteine“ erforderlich: Elektronen, Positronen und Polektronen. Zur Veranschaulichung wird darauf hingewiesen, daß zahlreiche Meßmethoden für elektrische Ströme aufgrund der Wirkungen außerhalb des metallischen Leiters funktionieren. Dies wird durch die Modellvorstellung verständlich: Die Messung basiert auf der Erfassung des Bewegungsvorganges der Polektronen, der als magnetische Wirkung in Erscheinung tritt.

Mit dieser Darstellung lassen sich auch Reflexionen an langen Doppelleitungen (Lecher-Leitungen) in einfacher Weise erklären, und zwar sowohl bei am Ende offener als auch bei am Ende kurzgeschlossener Doppelleitung (RÜDENBERG 1962).

c) Elektrischer Strom in einem langen geraden Leiter

Bei herkömmlichen theoretischen Ansätzen wird ein langer gerader Stromleiter ohne jegliche Berücksichtigung der Einspeisepunkte dargestellt. Alternativ wird auch ein differentielles Stromelement angenommen, das durch Integration in einen langen geraden Leiter überführt werden kann. Aber auch hierbei fehlen im Ansatz die Einspeisepunkte. Durch die Modellvorstellung läßt sich auch der Sachverhalt mit Einspeisepunkten in einfacher Weise beschreiben (BILD 4).

---

BILD 4

---

Die drei „Bausteine“ Elektron, Positron und Polektron wandern zunächst in der Zuführungs- Doppelleitung bis zu den Einspeisepunkten. Nun laufen die Elektronen beispielsweise nach rechts und die Positronen nach links. Die Polektronen-Ketten (FARADAY-sche Kraftlinien) bilden Bögen, die sich im wesentlichen radial von den Einspeisepunkten mit Lichtgeschwindigkeit weg bewegen.

Irgendwo weit draußen sind die Enden des „langen geraden Leiters“ durch eine Rückleitung kurzgeschlossen, so daß jetzt ein rückläufiger Vorgang einsetzt, wobei Elektronen und Positronen jeweils auf dem anderen Leiter zurückkehren. Dabei kehrt sich die Richtung des – als Polektron bezeichneten – elektro-statischen Elementar-Dipols um und entsprechend erfolgt auch eine Umkehr des Richtungssinnes der Polektronen-Ketten, wie es sinngemäß für die FARADAY-schen elektrischen Kraftlinien bekannt ist.

Gleichzeitig kehrt sich aber auch die mit Lichtgeschwindigkeit (relativ zum Leiter) erfolgende Bewegungs-Richtung um und die resultierende Wirkung bleibt dieselbe wie auf dem „Hinweg“. Diese Wirkung ist das, was normalerweise als magnetische Feldwirkung bezeichnet wird. Es handelt sich aber hierbei nicht um einen ruhenden Zustand, sondern um einen dynamischen Vorgang entsprechend einer „stehenden Welle“.

d) Gerader Sende-Dipol

Nun ist der Übergang auf einen geraden Sende-Dipol nicht mehr schwer. Wir betrachten dazu wieder das BILD 4. Sind nämlich die Enden des langen geraden Leiters nicht kurzgeschlossen, so tritt an den Enden eine Reflexion der Elektronen und Positronen entsprechend einer Reflexion einer Spannungs-Wanderwelle im herkömmlichen Sprachgebrauch auf. Elektronen und Positronen kehren auf demselben Leiter zu den Einspeisepunkten zurück und führen die Polektronen-Ketten im rückläufigen Sinne mit sich. Die Polarisation der Polektronen-Ketten bleibt erhalten, die Bewegungsrichtung ist umgekehrt. Die magnetische Wirkung beider Teilvorgänge ergänzt sich zu Null. Ist an der Zuführungs-Doppelleitung eine Gleichspannungs-Quelle angeschlossen, so stellt sich ein stationärer Zustand ein, der einem geladenen Kondensator entspricht. Dies wurde schon im Zusammenhang mit BILD 2 erklärt.

Es wird jedoch nunmehr deutlich, wie die Polektronen-Ketten ursächlich in den Einflußbereich der Kondensator-Platten gelangt sind. Denn der Kondensator mußte ja zu seiner Aufladung zunächst an eine Zuführungs-Doppelleitung angeschlossen werden. Seine Aufladung erfolgte also mit Elektronen. Positronen und Polektronen über die Doppelleitung.

Wird nun aber eine Wechselspannungs-Quelle an die Zuführungs-Doppelleitung angeschlossen, so ergibt sich ein periodischer Vorgang, bei dem die Polektronen-Ketten von den Einspeisepunkten weg und wieder zu diesen zurück pulsieren. Man kann sie angenähert mit Seifenblasen vergleichen, die sich nicht vom Blasrohr ablösen, aber periodisch aufgeblasen und wieder luftfrei gemacht werden. Die Seifenblasen können sich aber auch ablösen und in den Raum hinauswandern, wenn eine geeignete Zuordnung zwischen Blase-Rhythmus und Oberflächenspannung der Seifenblasen eingehalten wird. Und genau dieser Vorgang tritt nun offenbar bei den elektro-magnetischen „Wellen“ auf, wie es in BILD 5 verdeutlicht wird.

Auch die Polektronen-Ketten besitzen eine „Elastizität“, wie sie bei den „FARADAY-schen Kraftlinien“ schon Anfang des vorigen Jahrhunderts beobachtet wurden. Wichtig ist aber auch, daß die Polektronen-Ketten, wenn man sie „aufschneidet“, jeweils mit ungleichnamigen Polaritäten enden, so daß ein „Zusammenkleben“ zu geschlossenen Ringen aufgrund der elektrostatischen Anziehungskraft jederzeit möglich ist. Diese geschossenen Ringe wandern nun aufgrund ihrer Massen-Trägheit mit Lichtgeschwindigkeit relativ zum erregenden Leiter in den Raum hinaus. Denn die Masse eines Polektrons war mit der doppelten Elektronen-Masse im Rahmen der Modellvorstellung vorausgesetzt worden. Bei Lichtfrequenzen entsprechen die geschlossenen Polektronen-Ringe den von EINSTEIN postulierten Lichtquanten, die den korpuskularen Charakter des Lichtes repräsentieren.

---

    BILD 5                                                            BILD 6            

---

e) Gerader Empfangs-Dipol

Wird nun gemäß BILD 6 ein gerader Empfangs-Dipol in den Bereich der Polektronen-Ketten gebracht, so läßt sich erstens eine elektrische Spannung wechselnden Vorzeichens messen, denn die Polarisation der Ringe wechselt beim stetigen Durchlauf am Ort des Empfangs-Dipols. Es läßt sich zweitens eine kinematische Wirkung feststellen aufgrund des Aufpralls der Polektronen auf den Empfangs-Dipol („Licht-Druck“). Und drittens werden, falls der Empfangs-Dipol über einen Strommesser geschlossen wird, die Polektronen – durch den Aufprall in Elektronen und Positronen gespalten – einen elektrischen Stromfluß verursachen. Auf diese Weise liefert die Modellvorstellung in höchst einfacher Weise alle drei Phänomene, die bisher beobachtet und nur widersprüchlich erklärt werden konnten. Dabei ist gleichzeitig der sogenannte „Dualismus“ zu einer leicht deutbaren Erscheinung geworden.

In entsprechender Weise erklärt sich auch das FARADAY-sche „Induktions-Gesetz“, das die in einem geschlossenen Leiterkreis beobachteten elektrischen Spannungen bei Wechselerregungen niedriger Frequenzen beschreibt. Ein Unterschied besteht insofern, als hierbei nur das sog. Nahfeld wirksam wird, bei dem die Polektronen-Ketten hin-rückläufige Bewegungen mit Lichtgeschwindigkeit relativ zum Leiter ausführen, bedingt durch die bereits besprochene „Elastizität“ der Ketten entsprechend den FARADAY-schen Kraftlinien. Diese Hin-Rückläufigkeit läßt sich mit den bisherigen Theorien nicht beschreiben, ist aber durch die Messung von Wirk- und Blindleistungen, z. B. an Sende-Dipolen, experimentell belegbar.

f) Magnetische Abstoßungs- und Anziehungskräfte

Alle magnetischen Kräfte – auch die eines Dauermagneten – sind von elektrischen Kreisströmen (Gleichstrom-Erregungen) abhängig darstellbar. Diese Kreisströme erzeugen eine Art „stehender Wellen“, deren „Wellenfrequenz“ durch die „Umlauffrequenz“ der Kreisströme bestimmt ist. Im Rahmen der Modellvorstellung ergeben sich dabei hin-rückläufig bewegte Polektronen-Ketten, wie es schon im Zusammenhang mit dem Nahfeld im vorhergehenden Abschnitt e) angedeutet wurde. Dadurch lassen sich sowohl magnetische Abstoßungs- als auch Anziehungskräfte in einfacher Weise mit der Modellvorstellung erklären, wie bei FRIEBE (1985), S. 36/37, näher erläutert ist.

g) Ausblick

Die vorstehenden Ausführungen zeigen, daß eine einfache Modellvorstellung alle wesentlichen elektro-magnetischen Erscheinungen auf klassische Weise zu erklären gestattet. Wesentlich ist hierbei die Beschreibung der „elektrischen Kraftlinien“ nach FARADAY als materielle, korpuskular aufgebaute Ketten von Elementarteilchen, die als Polektronen bezeichnet werden. Jedes Polektron stellt dabei eine Paarbildung von einem Elektron und einem Positron dar.

Ferner ist wesentlich, daß magnetische Erscheinungen als dynamische Vorgänge betrachtet werden, deren zeitliches Verhalten entscheidend ist. Herkömmliche Methoden, von denen auch die MAXWELL-sche Theorie ausgeht, beschreiben einen elektrischen Strom als unendlich kleines Stromelement, das keine raum-zeitliche Verknüpfung mit der Stromquelle besitzt. Dadurch ergibt sich in der mathematischen Beschreibung eine Uneindeutigkeit des zeitlichen Ablaufs, die auch durch Integration nicht überbrückt werden kann. Dies hat zahlreiche Schwierigkeiten der derzeitigen Elektrodynamik zur Folge.

Mit der neuen Modellvorstellung wird dieser Nachteil vermieden und erstmalig eine Beschreibung vorgeschlagen, die dem Prinzip „actio = reactio“ gerecht wird. Dieses Prinzip, das nicht nur bei klassisch-mechanischen, sondern auch bei elektro-statischen und magnetischen Vorgängen zweifelsfrei durch die Erfahrung bestätigt ist, ist unabdingbare Voraussetzung, um Kraft-, Energie- und Leistungszuordnungen im Bereich der Elektrodynamik fehlerfrei zu beschreiben.

 

h) Literatur

FRIEBE, E. (1985): „Analyse des physikalischen Aussagegehalts der MAXWELL-schen Elektrodynamik“, DABEI-Colloquium, Heft 2, Bonn.

FRIEBE, E. (1987): „Irrtümer in der Elektronen-Theorie? Zeitschrift raum&zeit  –  „Ist die Elektronen-Theorie die eigentliche Ursache zahlreicher Schwierigkeiten der Theoretischen Physik?“, DPG-Didaktik-Tagungsband 1987, S. 405 – 410. Hrsg.: Prof. Dr. Wilfried KUHN, Gießen.

FRIEBE, E. (1991): „Innovationshemmende Dogmen in den Naturwissenschaften“, DABEI-Jahrestagung, Bonn, 16. – 18. 5. 91 (DABEI-Mitglieder-Manuskript DMM 85).

FRIEBE, E. (1992): „Das Dogma der Lichtgeschwindigkeit als Grenzgeschwindigkeit“, DPG-Didaktik-Tagungsband 1992, S. 552 – 555. Hrsg.: Deutsche Physikalische Gesellschaft.

KOPPELMANN, G. / HENSEL, N. (1988): „Atom-Cluster und Kristalle – Teilchen im Übergangsgebiet zwischen Atom- und Festkörperphysik“, DPG-Didaktik-Tagungsband 1988, S. 105 – 118. Hrsg.: Prof. Dr. Wilfried KUHN, Gießen.

MEYA, J. (1990): „Elektrodynamik im 19. Jahrhundert – Rekonstruktion ihrer Entwicklung als Konzept einer redlichen Vermittlung“, Deutscher Universitäts-Verlag, Wiesbaden.

RÜDENBERG, R. (1962): „Elektrische Wanderwellen“, 4. Auflg., Verlag Springer, Berlin – Göttingen – Heidelberg.

---

• Homepage

 

---

FRIEBE, E. (1991): „Mißbrauch der Mathematik“,

DABEI-Mitglieder-Manuskript DMM 86

Der Autor nachstehender Denksportaufgabe hatte als Kritiker im Jahre 1980 wegen mutmaßlicher Irrtümer in der Albert EINSTEIN zugeschriebenen speziellen Relativitäts-Theorie einen Physik-Professor der Ludwig-Maximilians-Universität München angeschrieben. Dieser Professor war damals gerade in den Ruhestand getreten und ist inzwischen schon verstorben. Seine ersten Gegenargumente, die sich auf sogenannte „experimentelle Bestätigungen“ bezogen, konnten den Kritiker nicht überzeugen. Denn zur Auswertung der diskutierten Experimente wurde eine Formel aus der Elektrizitätslehre als richtig unterstellt, die lediglich theoretisch formuliert aber ihrerseits niemals experimentell überprüft worden war.

Daraufhin versuchte der Herr Professor mit Schreiben vom 16.10.1980 einen mathematischen Beweis der Richtigkeit der sogenannten „Geschwindigkeitsabhängigkeit der Masse“ zu erbringen. Die entsprechende mathematische Ableitung hatte er zu diesem Zweck handschriftlich erstellt. Sie war sehr klar aufgebaut und enthielt nur einfache Annahmen aus der klassischen Mechanik. Ein Äther (Lichtmedium) war nicht als gegeben vorausgesetzt.

Da der Kritiker sich seiner eigenen mathematischen Kenntnisse nicht so sicher war, analysierte er die gegebene Ableitung nach erkenntniswissenschaftlichen Gesichtspunkten. Er erkannte, daß die Ableitung keinerlei spezifische Gesichtspunkte des Elektro-Magnetismus, der Optik oder der Atom- und Quantenphysik enthielt und genau so gut auf rein klassische Probleme anwendbar war. Er formulierte daher eine GLOSSE, die nachstehend in überarbeiteter Form als „Denksportaufgabe“ wiedergegeben ist. Diese GLOSSE sandte er dem Herrn Professor mit einem kurzen Begleitschreiben vom 30. 3. 1981, in dem es unter anderem hieß (Zitat):

„Betrachten Sie diese GLOSSE bitte ausschließlich als einen der Klarstellung dienenden, unkonventionellen Beitrag zur Lösung des „Gordischen Knotens“ der speziellen Relativitäts-Theorie. Sie werden sehen, es handelt sich um eine höchst interessante Denksportaufgabe. Ich stelle Ihnen anheim, diese GLOSSE Ihren Fachkollegen zur kritischen Stellungnahme zur Verfügung zu stellen.“

Der Kritiker kannte damals selbst keine stichhaltige Lösung des hier angeschnittenen Problems. Seine erste Vermutung erwies sich als unhaltbar. Aber auch der Herr Professor konnte keine überzeugende Erklärung abgeben. Er beschränkte sich daher im wesentlichen auf geschichtliche Erläuterungen, in denen es unter anderem hieß (Zitat):

„Übrigens hat dies“ (gemeint ist die diskutierte mathematische Ableitung) „schon LENARD gewußt, der etwa bis 1918 Anhänger EINSTEINs (und nicht nur seiner Theorie) war. Er war ehrlich genug, die relativistischen Bewegungsgleichungen in seiner sogenannten Deutschen Physik aus W = m · c² abzuleiten. Anscheinend hat er es nicht gesehen, jedenfalls hat er es nicht gesagt, daß er einen neuen und sehr einfachen Zugang zur Relativitäts-Theorie gefunden hat. Denn auf dem neuen Weg ist man nicht mehr mit dem Problem der Konforminvarianz konfrontiert.“

Der Autor wünscht dem Leser viel Spaß an der nun folgenden „Denksportaufgabe“. Vermutlich sind mehrere grundsätzliche Irrtümer enthalten. Der Autor kennt bisher mindestens einen Fehler. Dieser wird aber noch nicht verraten!

Denksportaufgabe

Energiegewinnung aufgrund der „Äquivalenz von Masse und Energie“

Eine originelle Alternative zur Lösung des Energieproblems

Wie zahlreichen Lehrbüchern zu entnehmen ist, hat Albert Einstein in den Jahren 1905/1906 im Rahmen seiner speziellen Relativitäts-Theorie gezeigt, daß Masse und Energie als äquivalent angesehen werden können. Die Formel

(1)

(mit W_o = Ruheenergie, m_o = Ruhemasse,

c² = Quadrat der Vakuum-Lichtgeschwindigkeit = absolute Konstante)

wird in der Atomphysik seit langem verwendet.

Im folgenden wird nun gezeigt, daß das oben genannte Äquivalenzprinzip viel allgemeinere Bedeutung besitzt. Dabei soll – wie es heute in der Theoretischen Physik allgemein gefordert wird – ausschließlich auf streng mathematische Beweise zurückgegriffen werden.

Vorausgesetzt sei ein mit Benzin (oder einem anderen chemischen Brennstoff) angetriebenes Fahrzeug (Kraftfahrzeug, Flugzeug, Schiff, Rakete, Raumfahrzeug) üblicher Bauart. Der Brennstoff (z. B. Benzin) besitzt einen potentiellen chemischen Energieinhalt W, der der Brennstoff-Masse m proportional ist. Es gilt daher:

(2)

K stellt dabei die Heizwert-Konstante des verwendeten Brennstoffs dar. Es besteht also eine Analogie zwischen den Glgn. (1) und (2), lediglich die Konstante c² ist durch die Heizwert-Konstante K ersetzt worden.

Durch beidseitige Differentiation der Glg. (2) nach der Zeit erhält man die Fahrzeugleistung (Verluste vernachlässigt):

(3)

NEWTONs Impulsgleichung lautet (Vektoren sind durch einen Pfeil gekennzeichnet):

(4)

(mit  n  =  Geschwindigkeit).  NEWTONs Kraftgleichung lautet bezogen auf den Impuls (die einfache Zuordnung: Kraft = Masse mal Beschleunigung ist hier nicht zulässig, da die Masse gemäß (3) zeitlich veränderlich ist):

(5)

Energieänderung = Leistung:

(6)

Nach (3) folgt aus (6):
(7)

Nach Multiplikation mit m erhält man aus (7) mit (4):

(8)

Die beidseitige Integration (mit „const“ = Integrations-Konstante) führt auf:

(9)

Definition: Beim Impuls  p = 0  sei die Masse  =  m₀ .  Substitution in (9):

(10)

Elimination der Konstanten aus (9/10):

(11)

Daraus folgt mit (4):
(12)

Also folgt für die Masse:
(13)

Mit (4) ergibt sich ferner als Impuls:
(14)

Schließlich ergibt sich mit (2) als Energie:

(15)

Es ergibt sich also für die Masse, den Impuls und die Energie eine analoge Abhängigkeit wie bei der speziellen Relativitäts-Theorie [vergleiche hierzu: FLEISCHMANN, Rudolf (1980): „Einführung in die Physik“, 2. Auflg., Physik Verlag, Weinheim, Abschnitt 6.1.6., Seite 500]. Hierbei ist lediglich der Wert c² (Quadrat der Vakuum-Lichtgeschwindigkeit) durch den Wert K ersetzt, der die Heizwert-Konstante des verwendeten Brennstoffs darstellt. Im Gegensatz zur Größe c, die eine absolute Konstante ist, ist K eine frei wählbare Konstante zwischen Null und einem Größtwert, der durch den spezifisch besten Brennstoff festgelegt ist. Bei K = 0 ergibt sich, daß die Geschwindigkeit n = 0 nicht überschritten werden kann, d. h. bei einem Heizwert Null des Brennstoffs kann das Kraftfahrzeug nicht fahren, was im Einklang mit der Erfahrung steht. Andererseits folgt – wie bei der Relativitäts-Theorie – , daß die Geschwindigkeit n einen Grenzwert nicht übersteigen kann, bei dem Masse, Impuls und Energie dem Wert Unendlich zustreben.

Bisher wurde stillschweigend vorausgesetzt, daß die Masse des Kraftfahrzeugs selbst gegenüber der Brennstoff-Masse vernachlässigbar sei. Diese Einschränkung kann nunmehr fallengelassen werden. Es ist in GIg. (2) folgender Wert (statt m) einzusetzen:

m _b = m – m _f – m _n

Hierbei bedeuten:

m = Gesamt-Masse

m _b = Brennstoff-Masse

m _f = Fahrzeug-Masse

m _n = Nutzlast-Masse

Beim Übergang von Glg. (2) auf Glg. (3), d. h. durch Differentiation, fallen die Größen m _f und m _n wieder heraus, da sie – im Gegensatz zur Brennstoff-Masse – konstant sind. Denn sie lassen sich nicht in Energie umsetzen. Die Glg. (3) gilt also unverändert im allgemeinen Falle, d. h. bei Berücksichtigung aller nicht aktiven Massen.

Wie aus Glg. (15) hervorgeht, ist in jedem Falle ein erheblicher Energiegewinn zu erzielen, denn die Brennstoff-Masse nimmt mit der Geschwindigkeit n des Fahrzeuges überproportional zu, gerade so, als ob wohlgesinnte Heinzelmännchen den Brennstoff-Tank ständig randvoll nachfüllen!

Oder sollte ein Fehler unterlaufen sein? Oder gar mehrere??? Was meinen SIE dazu?

LITERATUR
——————————————————————————————————

• Homepage

Der CARNOTsche Wirkungsgrad
– Ein folgenschwerer Irrtum –
FRIEBE, Ekkehard (1991)
DPG-Didaktik-Tagungsband 1991, S.489 – 500. Hrsg. Prof. Dr. Wilfried Kuhn, Gießen

A. Zusammenfassung

Der CARNOTsche Kreisprozeß beschreibt einen geschlossenen thermodynamischen Kreisprozeß, der durch zwei Isothermen und zwei Adiabaten (Isentropen) begrenzt ist. Bei der Ableitung des Wirkungsgrades hierzu wurde jedoch die stets vorhandene Umgebungs-Temperatur irrtümlich übersehen. Die Umgebung wirkt als SEHR GROSSER thermischer Speicher, der als Temperatur-Bezugs-Niveau die Grenze zwischen positiven und negativen Temperatur-Differenzen und Energieflüssen darstellt. Die Richtigstellung des Irrtums führt – nicht nur beim CARNOTschen Prozeß – zu wesentlich höheren Wirkungsgraden gegenüber Lehrbuch-Aussagen, und zwar vor allem bei niedrigen Temperaturen. Der mehr als 130 Jahre alte Irrtum bildet die Grundlage des sog. „Zweiten Hauptsatzes der Thermodynamik“ und ist als wissenschaftliches Dogma für die derzeitige „Klima-Katastrophe“ mitverantwortlich.

B. Veranlassung

In den letzten Jahren wurde in zunehmendem Maße auf Probleme der klassischen, noch heute gelehrten theoretischen Thermodynamik aufmerksam gemacht. Es sei hier insbesondere auf BARTH (1962, 1975, 1986, 1987), BLÖSS (1985), HILSCHER (1981, 1986), KIRCHHOFF (1986, 1987, 1990) und TRUESDELL (1980) verwiesen. Eine Überprüfung der Argumente der Kritiker hat die Richtigkeit der meisten Einwände ergeben (vgl. FRIEBE 1987, 1988, 1990). Nachstehend soll nun der grundlegende Irrtum klar herausgestellt werden.

C. Geschichtlicher Rückblick

Der sogenannte „CARNOTsche Wirkungsgrad“ der Thermodynamik bezieht sich auf Wärmekraft-Maschinen, bei denen es darum geht, die bei Erwärmung von Arbeitsmitteln (insb. Gasen, ggf. auch Festkörpern) auftretenden Druckänderungen zur Verrichtung von mechanischer Arbeit zu nutzen. Es ist also das Ziel, die in der Wärme enthaltene Wärme-Energie in mechanische Energie umzuwandeln. Das soll mit möglichst geringen Verlusten, d. h. mit einem möglichst hohen Wirkungsgrad geschehen. Die Bestimmung des Wirkungsgrades ist deshalb ein wesentliches Anliegen der theoretischen und praktischen Thermodynamik. – Grundlage der noch heute gelehrten Thermodynamik ist ein Buch von CARNOT (1824): „Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance“. Vorliegend wird auf die deutsche Übersetzung von OSTWALD (1909) Bezug genommen: „Betrachtungen über die bewegende Kraft des Feuers und die zur Entwickelung dieser Kraft geeigneten Maschinen“. Diese Arbeit behandelt – qualitativ und quantitativ – wesentliche Probleme der Thermodynamik. Sie bringt sogar eine einführende mathematische Ableitung der Beziehungen zwischen Temperatur, Druck und Volumen des verwendeten Arbeitsmittels. Eine Formel für den Wirkungsgrad findet man aber hierin nicht! Diese wurde erst von CLAUSIUS entwickelt. Hierauf hat schon KIRCHHOFF (1986, S. 26) hingewiesen.

Betrachten wir nun den „CARNOTschen Kreisprozeß“, wie ihn CARNOT selbst qualitativ beschreibt (Zitat einschl. Fig. 1 aus CARNOT 1824/1909, S. 20 – 22, ohne Anmerkungen):

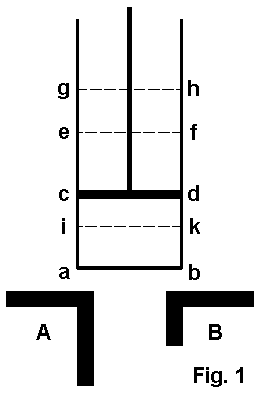
„Nachdem diese vorläufigen Punkte festgestellt worden sind, denken wir uns eine elastische Flüssigkeit, z. B. atmosphärische Luft in einem cylindrischen Gefäss a b c d , Fig. 1, mit einer beweglichen Scheidewand oder einem Kolben c d enthalten; wir denken uns ferner zwei Körper A und B , von denen jeder bei einer constanten Temperatur erhalten wird, wobei die von A höher sei, als die von B; wir stellen uns nun die nachstehend beschriebene Reihe von Operationen vor.

1. Berührung des Körpers A mit der im Raume a b c d enthaltenen Luft, oder mit der Wandung dieses Raumes, von welcher wir annehmen, dass sie die Wärme leicht durchlässt. Die Luft befindet sich vermöge dieser Berührung bei der Temperatur des Körpers A; c d sei die augenblickliche Stellung des Kolbens.

2. Der Kolben erhebt sich stetig und nimmt die Stellung e f ein. Zwischen dem Körper A und der Luft bleibt fortwährend Berührung bestehen, wodurch die Luft während der Ausdehnung bei constanter Temperatur erhalten wird. Der Körper A liefert den nötigen Wärmestoff, um die Temperatur constant zu halten.

3. Der Körper A wird entfernt und die Luft befindet sich nicht mehr in Berührung mit einem Körper, welcher ihr Wärmestoff liefern kann; der Kolben setzt indessen seine Bewegung fort und geht aus der Stellung e f in die Stellung g h . Die Luft wird verdünnt, ohne Wärmestoff aufzunehmen, und ihre Temperatur sinkt. Wir nehmen an, dass sie bis zu der des Körpers B sinkt; in diesem Augenblick bleibt der Kolben stehen und befindet sich in g h .

4. Die Luft wird nun in Berührung mit dem Körper B gesetzt; sie wird durch Senkung des Kolbens weiter comprimirt, indem man ihn aus der Stellung g h in die Stellung c d bringt. Dabei bleibt die Luft aber bei constanter Temperatur, weil sie den Körper B berührt, dem sie ihren Wärmestoff abgiebt.

5. Nachdem der Körper B entfernt ist, setzt man die Compression der Luft fort, welche in ihrem isolirten Zustande eine Temperaturerhöhung erfährt; Die Compression wird fortgesetzt, bis die Luft die Temperatur des Körpers A angenommen hat. Der Kolben bewegt sich während dieser Zeit aus der Stellung c d in die Stellung i k .

6. Die Luft wird mit dem Körper A in Berührung gebracht; der Kolben kehrt aus der Lage i k in die Lage e f zurück; die Temperatur bleibt unverändert.

7. Die unter 3. beschriebene Periode wiederholt sich, sodann die Perioden 4, 5, 6, 3, 4, 5, 6, 3, 4, 5 u. s. w.

Bei diesen verschiedenen Operationen erfährt der Kolben einen grösseren oder geringeren Druck von Seiten der im Cylinder eingeschlossenen Luft; die elastische Kraft dieser Luft ändert sich theils infolge der Volumänderungen, theils infolge der Temperaturänderungen; man muss aber darauf achten, dass bei gleichem Volum, d. h. bei gleicher Lage des Kolbens die Temperatur während der Ausdehnungsbewegung höher ist, als bei der Compressionsbewegung. Daher ist während der ersteren die elastische Kraft der Luft grösser, und somit die durch die Ausdehnungsbewegung hervorgebrachte bewegende Kraft beträchtlicher als die, welche zur Erzeugung der Compressionsbewegung verbraucht worden ist. Man erhält also einen Überschuss an bewegender Kraft, welchen man zu beliebigen Zwecken verwerthen kann. Die Luft hat uns als Wärmemaschine gedient; wir haben sie sogar auf die möglichst vortheilhafte Weise benutzt, weil keine unbenutzte Wiederherstellung des Gleichgewichts des Wärmestoffes stattgefunden hat.

Alle oben beschriebenen Vorgänge können in einem Sinne ebenso wie in umgekehrter Ordnung hervorgebracht werden. Denken wir uns nach der sechsten Periode, d. h. nachdem der Kolben in die Stellung e f gelangt ist, man ihn in die Stellung i k zurückgehen lässt, während man gleichzeitig die Luft in Berührung mit dem Körper A erhält; der während der sechsten Periode von diesem gelieferte Wärmestoff kehrt zu seiner Quelle, d. h. zum Körper A zurück und die Sachen befinden sich in dem Zustande, wie am Ende der fünften Periode. Entfernt man nun den Körper A und bewegt man den Kolben von e f nach c d , so wird die Temperatur der Luft um eben so viele Grade sinken, wie sie in der fünften Periode gestiegen war, und wird gleich der des Körpers B werden. Man kann offenbar eine Reihe von Operationen erfolgen lassen, welche alle die Umkehrung der oben beschriebenen sind; es genügt, sich unter dieselben Umstände zu versetzen, und für jede Periode eine Ausdehnungsbewegung statt einer Compressionsbewegung auszuführen, und umgekehrt.

Das Ergebnis der erstgenannten Operationen war die Erzeugung einer gewissen Menge bewegender Kraft und die Uebertragung von Wärmestoff aus dem Körper A in den Körper B ; das Ergebnis der umgekehrten Operationen ist der Verbrauch der erzeugten bewegenden Kraft und die Rückführung des Wärmestoffs von B nach A , so dass die beiden Arten von Operationen einander aufheben, einander sozusagen neutralisiren.“ (Ende des Zitats)

In diesem Zusammenhang ist auch der von CARNOT auf Seite 23 aufgestellte Satz von besonderer Bedeutung (Zitat aus CARNOT 1824/1909):

„Die bewegende Kraft der Wärme ist unabhängig von dem Agens, welches zu ihrer Gewinnung benutzt wird, und ihre Menge wird einzig durch die Temperaturen der Körper bestimmt, zwischen denen in letzter Linie die Ueberführung des Wärmestoffes stattfindet. Es ist hierbei vorausgesetzt, dass jede der Methoden, die bewegende Kraft zu gewinnen, die Vollkommenheit erreicht, deren sie fähig ist. Diese Bedingung ist erfüllt, wenn, wie oben erwähnt, keine anderen Temperaturänderungen in den Körpern stattfinden als solche, die durch Volumänderungen hervorgerufen werden, oder, was dasselbe in anderer Ausdrucksform ist, wenn niemals eine Berührung zwischen Körpern von merklich verschiedener Temperatur stattfindet.“ (Ende des Zitats)

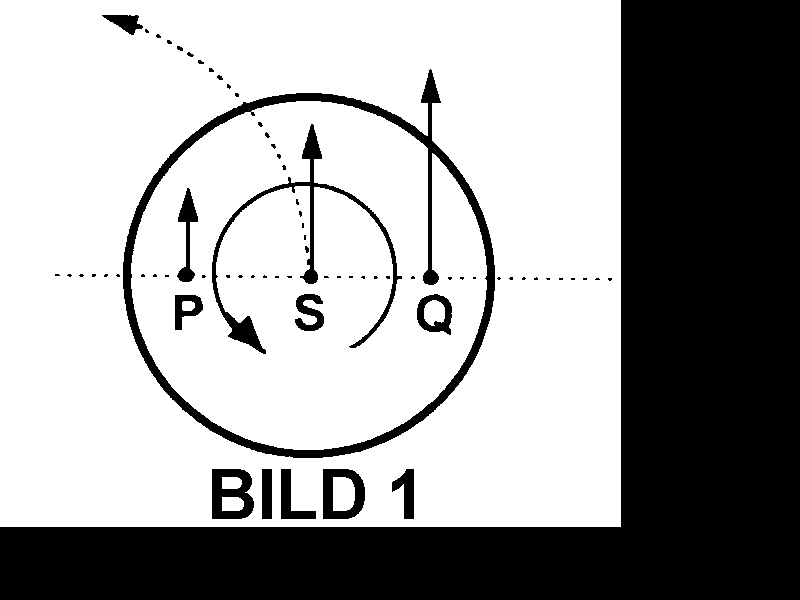
CARNOT macht hier deutlich, daß er einen idealisierten Kreis-Prozeß beschreibt, bei dem alle Temperatur-Gefälle vernachlässigt werden. Unausgesprochen setzt er auch voraus, daß Wärmeverluste durch Abstrahlung und Ableitung nicht auftreten sollen. Er erkennt klar, daß unter diesen Voraussetzungen die Kältemaschine (heute vielfach als Wärmepumpe bezeichnet) die direkte Umkehrung der Wärme-Kraftmaschine ist und daß beide Maschinen vollkommen gleichwertig sind. In beiden Fällen wird eine 100 %ige Umsetzung von „Wärmestoff“ in „bewegende Kraft“ und umgekehrt gefolgert. CARNOT beschreibt hier auf seine Weise – unter Hinweis auf die Unmöglichkeit eines perpetuum mobile (S. 13/14 seiner Arbeit) – was später als Energie-Erhaltungs-Prinzip in die Naturwissenschaften eingegangen ist. Der Kreis-Prozeß nach CARNOT wird heute vorwiegend im sog. pV-Diagramm dargestellt, bei dem das Volumen als Abszisse und der Druck als Ordinate aufgetragen ist (BILD 1).

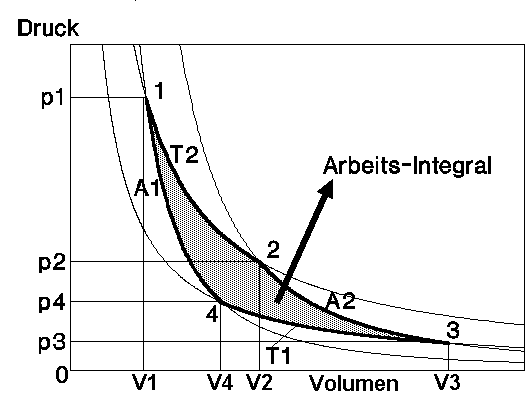
BILD 1: CARNOTscher Kreisprozeß, schematische Darstellung.

V = Volumen (Abszisse)
p = Druck (Ordinate)
A1 = untere Adiabate
A2 = obere Adiabate
T1 = Isotherme mit Temperatur T1 = const.
T2 = Isotherme mit Temperatur T2 = const. ( T2 > T1)

D. Der sogenannte „CARNOTsche Wirkungsgrad“

Wie bereits gesagt, hat CARNOT selbst eine Formel für den Wirkungsgrad nicht angegeben. Diese wurde erst von CLAUSIUS entwickelt.

Die auf CLAUSIUS (1887) zurückgehende Ableitung des sogenannten „CARNOTschen Wirkungsgrades“ erfolgt bei verschiedenen Autoren auf unterschiedliche Weise. Es wird beispielsweise auf CERBE / HOFFMANN (1982): „Einführung in die Wärmelehre“, Seiten 89 – 91, verwiesen.

Dort wird als Ergebnis angegeben (unter Anpassung der Indizes an unsere Definitionen gemäß vorstehendem BILD 1):

[1]              h = 1 – T1 / T2 = (T2 – T1) / T2

Vorstehende Beziehung [1] ist das allgemein anerkannte Ergebnis für den „CARNOTschen Wirkungsgrad“ (CARNOT-Faktor), der als der größtmögliche Wirkungsgrad für geschlossene thermische Kreisprozesse bezeichnet wird. Hieraus sind die umstrittenen Begriffe Entropie und Exergie abgeleitet worden.

Die Gleichung [1] besagt, daß ein Wirkungsgrad von 100 % nur erreichbar ist, wenn die Temperatur T1 des kälteren Körpers B (vgl. die Figur 1 von CARNOT) T1 = 0 ist, also auf dem absoluten Temperatur-Nullpunkt liegt. Bei praktisch realen Temperaturen ergeben sich vergleichsweise sehr geringe Wirkungsgrade. So erhält man z. B. bei T2 = 40° C und T1 = 20° C entsprechend T2 = 313° K und T1 = 293° K nur einen Wirkungsgrad von 6,4 %, obwohl alle technisch realen Verluste (vgl. Abschnitt F) voraussetzungsgemäß vernachlässigt worden sind.

Obgleich die Ableitung zu [1] im Rahmen der gegebenen Voraussetzungen mathematisch fehlerfrei ist, sind dennoch drei grundlegende physikalische Irrtümer enthalten. Hierauf soll im folgenden Abschnitt eingegangen werden.

E. Drei grundlegende physikalische Irrtümer

Es erhebt sich nun die FRAGE:
Wo liegen die grundlegenden Irrtümer in der genannten Ableitung?

Die ANTWORTEN lauten:

Irrtum 1.

Der CARNOT-sche Prozeß wird als geschlossener thermischer Kreisprozeß bezeichnet. Jedoch ist er lediglich geschlossen bezüglich des eingeschlossenen Arbeitsmittels (Gasmasse), nicht jedoch bezüglich der Wärmeenergie. Denn der „heiße“ Speicher (Körper A) muß dauernd nachgeheizt und der „kalte“ Speicher (Körper B) dauernd gekühlt werden, um die vorausgesetzte konstante Temperatur zu erhalten. Die mathematisch so elegante Annahme einer Temperatur-Konstanz der beiden Speicher ist also physikalisch vollkommen unvernünftig, da damit vorgetäuscht wird, die beiden Speicher befänden sich in einem statischen Zustand. In Wirklichkeit ist dauernd ein Energiefluß (Wärmestrom) gegeben, der einerseits von außen in den jeweiligen Speicher einströmt, andererseits an das Arbeitsmittel (Gasmasse) abgegeben wird. Die Speicher sind allerdings notwendig, um zeitliche Schwankungen des Energieflusses auszugleichen.

Irrtum 2.

Es wurde übersehen, daß Wärmeenergie bei dem hier betrachteten thermo-dynamischen Prozeß sowohl als statische Größe (Wärmeenergie = Temperatur mal Wärmekapazität) als auch als dynamische Größe (Wärmeenergie = Temperaturdifferenz mal Energiefluß) auftritt. Bei dem theoretischen Ansatz nach CLAUSIUS ist nur die statische Größe berücksichtigt entsprechend der Zustandgleichung für das ideale Gas:

p · V = m · R · T

p = Druck
V = Volumen
m = Masse der Gasfüllung
R = universelle Gaskonstante
T = absolute Temperatur

Hierbei kann die Konstante R als Wärmekapazität interpretiert werden.

Aus folgender Betrachtung geht nun hervor, daß die Wärmeenergie als dynamische Größe unberücksichtigt geblieben ist. Hierfür ist nämlich die folgende Voraussetzung von CARNOT wesentlich (siehe das oben gebrachte Zitat aus CARNOT 1824/1909, Seite 23):

„Es ist hierbei vorausgesetzt, dass jede der Methoden, die bewegende Kraft zu gewinnen, die Vollkommenheit erreicht, deren sie fähig ist. Diese Bedingung ist erfüllt, wenn, wie oben erwähnt, keine anderen Temperaturänderungen in den Körpern stattfinden als solche, die durch Volumänderungen hervorgerufen werden, oder, was dasselbe in anderer Ausdrucksform ist, wenn niemals eine Berührung zwischen Körpern von merklich verschiedener Temperatur stattfindet.“ (Ende des Zitats)

CARNOT ist sich hier offensichtlich bewußt, daß ein Energiefluß zwischen zwei Körpern nur bei einer endlichen Temperaturdifferenz möglich ist, daß aber die Vollkommenheit nur dann erreicht wird, wenn diese Temperatur-differenz sehr klein ist.

Im theoretischen Ansatz nach CLAUSIUS ist aber an keiner Stelle eine solche kleine Temperaturdifferenz eingeführt worden. Die Temperatur-differenz zwischen den Körpern ist vielmehr stillschweigend gleich NULL gesetzt worden, so daß ein thermischer Energiefluß gar nicht möglich ist.

Es hätte hier im Ansatz eine differentiell kleine Temperaturdifferenz eingeführt werden müssen, die dann in einem Grenzwertübergang zur angestrebten Vollkommenheit geführt hätte. Die NULL-Setzung im vorliegenden Fall nimmt jedoch der theoretischen Untersuchung jeden physikalisch realen Wert. Ein thermischer Energiefluß findet überhaupt nicht statt. Damit ist jede Aussage über Energiegrößen und Wirkungsgrade unmöglich.

Irrtum 3.

Bei der Integration über p·dV wurde die Umgebungs-Temperatur nicht berücksichtigt. Denn die Umgebung wirkt als sehr großer thermischer Energie-Speicher, der als Temperatur-Bezugs-Niveau die Grenze zwischen positiven und negativen Temperatur-Differenzen und Energieflüssen bildet und in die Rechnung mit einzubeziehen ist. Dieser Energie-Speicher dient nämlich zur thermischen „Abstützung“ der beiden von CARNOT vorausgesetzten wärmespeichernden Körper A und B (siehe Fig. 1 nach CARNOT).

Diesen grundlegenden Irrtum hat wohl BARTH als erster klar herausgestellt. In dem Buch von BARTH (1962): „Rationale Physik“ im Kapitel: „Wärme als eine Form der Energie“ wird auf Seite 256, zweiter Abs., ausgeführt (Zitat):

„Die Umsetzung mechanischer Energie in Wärmeenergie besteht notwendig in der Erhöhung der thermischen potentiellen Energie, in einer Erhöhung des thermischen Potentials. Jedoch nicht absolut genommen, sondern in der relativen Erhöhung des Potentials, in der Bildung einer Temperaturdifferenz. Die Energiebilanz wird allein durch diese Temperaturdifferenz bestimmt, nicht durch absolute Temperaturen. Eine Temperaturabnahme, also eine negative Temperatur gegen die Umgebung bedeutet ebenso eine Zunahme der thermischen potentiellen Energie wie eine Temperaturerhöhung. Beim Thomson-Jouleeffekt wird demnach in jedem Fall mechanische Energie in thermische Energie umgewandelt, gleichgültig ob nun das Gas sich erwärmt oder abkühlt. Die erzeugte Wärmeenergie ist allein bestimmt durch die entstandene Temperaturdifferenz (gegen die wirkliche Umgebung), aber nicht durch eine theoretische absolute Temperatur.“ (Ende des Zitats)

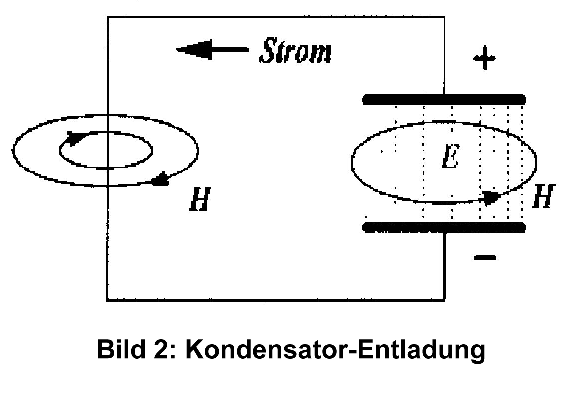
Zur Veranschaulichung dieses von BARTH zutreffend herausgestellten Sachverhaltes wird auf BILD 2 und BILD 3 verwiesen. Dabei ist die als konstant angenommene absolute Umgebungs-Temperatur mit Tu bezeichnet. Zu berücksichtigen ist allerdings, daß Tu in der Realität nie konstant ist (Winter, Sommer; Nacht, Tag usw.). Es ist hier ähnlich zu verfahren, wie bei mechanischen Niveau-Betrachtungen bezüglich der Meereshöhe über NN (Normal-Null). Denn auch die Meereshöhe ist in Wirklichkeit nicht konstant (z. B. Schwankungen durch Ebbe und Flut).

Ferner genügt es nicht, die Lufttemperatur in unmittelbarer Umgebung des betrachteten thermodynamischen Prozesses als Tu zu betrachten, denn die Lufttemperatur wird sehr schnell durch die Wärmeabgabe des Prozesses verändert werden. Es ist vielmehr dafür zu sorgen, daß ein dauernder, großräumiger Temperaturausgleich stattfindet. Es bieten sich daher für die Festlegung einer Normal-Umgebungs-Temperatur Tu die Weltmeere bei hinreichender Meerestiefe an.

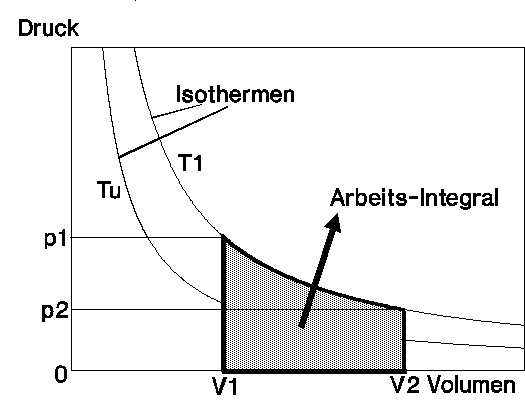
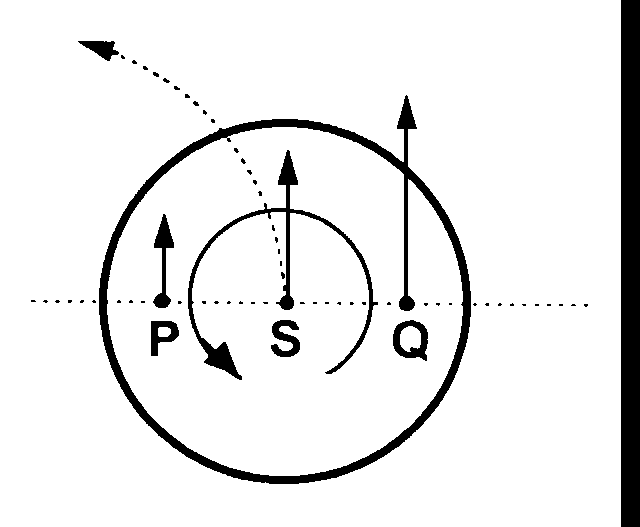
BILD 2: FALSCH ——- Arbeits-Integral unter der Isotherme.
V = Volumen (Abszisse) p = Druck (Ordinate) T1 = Isotherme mit Temperatur T1 = const. Tu = Isotherme mit der Umgebungs-Temperatur Tu
Tu = const. ( T1 > Tu )

Bei der genannten Ableitung wurde entsprechend BILD 2 das Arbeits-Integral unter der Isotherme irrtümlich gegenüber der absoluten Temperatur = NULL (Abszissen-Gerade) gebildet. Die Umgebungs-Temperatur Tu wurde fälschlich außer acht gelassen.

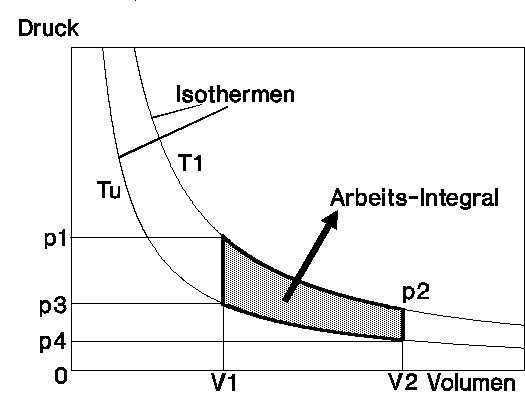
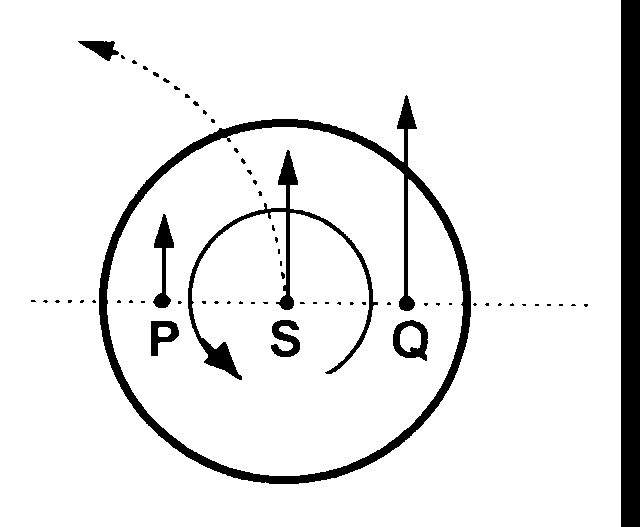
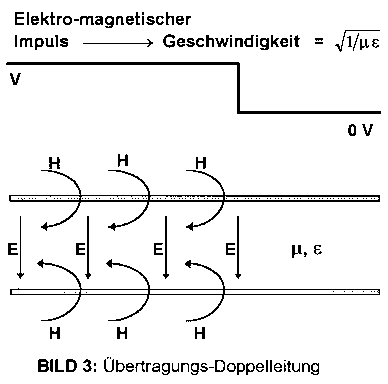
BILD 3: RICHTIG ——- Arbeits-Integral unter der Isotherme.
V = Volumen (Abszisse)
p = Druck (Ordinate)
T1 = Isotherme mit Temperatur T1 = const.
Tu = Isotherme mit der Umgebungs-Temperatur Tu
Tu = const. ( T1 > Tu )

BILD 3 verdeutlicht die richtige Bestimmung des Arbeits-Integrals. Diese richtige Integration ergibt ein wesentlich kleineres Arbeits-Integral. Das Entsprechende gilt auch für die Isotherme T2. Anschließend ist die Summe bzw. Differenz der Arbeits-Integrale unter T1 und T2 zu bilden.

Damit erhält man für den „CARNOTschen Wirkungsgrad“ h :

[2]              h = 1 – (T1 – Tu) / (T2 – Tu)

Hierbei ist die Voraussetzung von CARNOT wesentlich (siehe das oben schon gebrachte Zitat aus CARNOT 1824/1909, Seite 23):

„Es ist hierbei vorausgesetzt, dass jede der Methoden, die bewegende Kraft zu gewinnen, die Vollkommenheit erreicht, deren sie fähig ist. Diese Bedingung ist erfüllt, wenn, wie oben erwähnt, keine anderen Temperaturänderungen in den Körpern stattfinden als solche, die durch Volumänderungen hervorgerufen werden, oder, was dasselbe in anderer Ausdrucksform ist, wenn niemals eine Berührung zwischen Körpern von merklich verschiedener Temperatur stattfindet.“ (Ende des Zitats)

Über die Berücksichtigung von Verlusten, die außerhalb dieser Voraussetzung liegen, siehe den Abschnitt F.

In Glg. [2] sind nun folgende Sonderfälle enthalten:

1. T2 > T1, T1 > Tu

Bei diesem Fall sind – wegen T1 > Tu und T2 > T1 > Tu – beide Klammer-ausdrücke in [2] positiv und der Wirkungsgrad wird kleiner als 100 %. Der Kreisprozeß ist also verlustbehaftet. Dies folgt daraus, daß der kältere Speicher (Körper B gemäß Fig. 1 nach CARNOT) dauernd Wärme, die ihm bei jedem Zyklus zugeführt wird, an die Umgebung abgeben muß, um seine Temperatur zu halten.

2. T2 > T1, T1 = Tu
Hierbei ist die Temperatur des kälteren Speichers gleich der Umgebungs-Temperatur gewählt. Nun erhält man als Wirkungsgrad:

[3]              h = 1 – (T1 – T1) / (T2 – T1) = 1 = 100 %

Es treten also bei den gegebenen Voraussetzungen keinerlei Verluste auf. Glg. [3] stellt daher den optimalen Wirkungsgrad einer thermodynamischen Maschine dar. Dieses Ergebnis weicht entscheidend von Lehrbuchaussagen ab.

3. T2 > Tu, T1 < Tu

Hierbei ist die Temperatur des „kalten“ Speichers bewußt unterhalb die Umgebungstemperatur gelegt. Das gelingt natürlich nur, wenn dieser Speicher dauernd – unter Energieaufwand – gekühlt wird. Es ergibt sich:

[4]              h = 1 – (Tu – T1) / (T2 – Tu)

Dieser Kreisprozeß ist – wegen der erforderlichen Kühlung des „kalten“ Speichers – ebenfalls verlustbehaftet.

Das Ergebnis nach den Glgn. [2], [3] und [4] ist – ebenso wie bei der klassischen Formel für den „CARNOTschen Wirkungsgrad“ – unabhängig vom Umgebungs-Druck, so daß dieser auch durch eine konstante positive oder negative Vorlast in weiten Grenzen frei gewählt werden kann. Diese Unabhängigkeit von einer Vorlast erklärt sich dadurch, daß die Vorlast zwar bei dem einen Kolbenhub positive Arbeit, bei dem entgegengesetzten Kolbenhub aber eine gleich große negative Arbeit verrichtet. Dies trifft sogar bei einer Vorlast durch eine lineare oder nichtlineare mechanische Feder zu, da auch diese bei einem geschlossenen Zyklus im Ergebnis keine Arbeit verrichtet.

Es könnte jetzt der Einwand erhoben werden, daß die Glg. [3] unmöglich richtig sein könne, da doch zweifellos längs der Isotherme mit der Temperatur T1 Energie in den Speicher mit der Temperatur T1 abfließe. Diese Energie gehe dadurch „verloren“ und sei deshalb den Verlusten zuzurechnen. Hier liegt ein grundlegender Irrtum vor. Denn bei dieser Isotherme ist nicht nur der Energiefluß sondern auch die – voraussetzungsgemäß sehr kleine – Differenz-Temperatur zwischen Arbeitsmittel und äußerem Speicher negativ. Es ergibt sich also, da das Produkt zweier negativer Größen wieder positiv ist, für einen vollen Zyklus des CARNOTschen Kreisprozesses bei jeder der beiden Isothermen ein positiver thermischer Energie-Aufwand, der jeweils zu 100 % in mechanische Arbeit umgewandelt wird. Denn Energie ist stets das Produkt zweier Parameter, wie schon BARTH (1986, 1987) zutreffend ausgeführt hat. Bei Vernachlässigung aller Verluste ist daher der optimale Wirkungsgrad einer thermodynamischen Maschine gleich 100 % – in Übereinstimmung mit der Auffassung von CARNOT und im Gegensatz zu zahlreichen Lehrbuch-Darstellungen.

F. Berücksichtigung der Verluste

Aufgrund der Wirkungsgrad-Definition, die für mechanische, elektrische und thermische Prozesse in gleicher Weise gilt, ergibt sich der Wirkungsgrad h allgemein zu:

Wirkungsgrad h = Wab / Wzu = (Wzu – Vsu) / Wzu

Dabei bedeuten:
Wab = abgeführte Nutz-Energie
Wzu = zugeführter Energie-Aufwand
Vsu = Summe der Verluste

Die Bilanzierung: Wab = Wzu – Vsu ist gemäß Energie-Erhaltungs-Prinzip zwingend, auch wenn zunächst die Summe der Verluste nicht bekannt ist.

Die Verluste bei thermischen Prozessen sind im wesentlichen gegeben durch:

a) Verluste durch Wärme-Ableitung, Wärme-Abstrahlung und Wärme-Widerstände
b) Verluste durch mechanische Reibungen einschließlich Luftwirbel-Reibungen
c) Verluste durch pneumatische Undichtigkeiten, vor allem zwischen Kolben und Zylinder

Bei Berücksichtigung der Verluste ergibt sich stets ein Wirkungsgrad kleiner als 100 % , wenn „negative“ Verluste (z. B. Wärme-Einstrahlung von außen durch die Sonne) ausgeschlossen werden können. Die einzelnen Verluste müssen je für sich bestimmt und dann addiert werden, um die Summe der Verluste Vsu zu erhalten.

Das Bestimmen der Einzelverluste ist im allgemeinen nicht ganz einfach. Hier können im wesentlichen nur empirische Formeln verwendet werden. Dazu sind die für Ingenieure und Techniker bestimmten Handbücher zu verwenden. Vor allem wird auf das – zahlreiche Tabellen enthaltende – Buch von CERBE / HOFFMANN (1982), verwiesen, insb. auf den Abschnitt: „8. Wärmeübertragung“ (Seiten 245 bis 282).

G. Ausblick

Der zitierten Auffassung von CARNOT (siehe Abschnitt C.) kann man aus heutiger Sicht nahezu voll zustimmen. Einen Wirkungsgrad gibt CARNOT nicht an, da er einen idealisierten Kreisprozeß beschreibt, der bewußt so konzipiert ist, daß eine volle Umkehrbarkeit zwischen Wärme-Kraftmaschine und Kälte-Maschine (Wärmepumpe) gegeben ist.

Diese Voraussetzung schließt eine 100 %ige Umwandlung in beiden Richtungen mit ein. Dieser idealisierte Kreisprozeß hat zwar praktisch nur geringe Bedeutung, da er verlangt, daß der Prozeß nur äußerst langsam, d. h. quasistatisch, ablaufen darf. Aber die Betrachtungen hierzu von CARNOT sind – im Gegensatz zu denen von CLAUSIUS – folgerichtig durchgeführt.

So schließt sich denn der Kreis. Was CARNOT schon 1824 intuitiv richtig erkannt hatte, ist durch einen Irrtum in der nicht klar durchdachten Mathematik von CLAUSIUS verfälscht worden. Aus diesem Irrtum ergeben sich weitere Fehler. Wenn auch nur einer dieser Fehler unberücksichtigt bleibt, kommt es zu unüberbrückbaren Widersprüchen. Dadurch ist die Thermodynamik zu einer in sich widersprüchlichen Theorie geworden, die in dem sog. „Zweiten Hauptsatz der Thermodynamik“ gipfelt und die seit mehr als 130 Jahren als wissenschaftliches Dogma die Lehrbücher belastet.

Die Folgen des behandelten Irrtums sind weit größer, als es zunächst erscheinen mag. Der ursächliche Zusammenhang der fehlerhaften Thermodynamik mit der derzeit diskutierten „Klima-Katastrophe“ wird wohl erstmals klar von KIRCHHOFF (1990) herausgestellt. Das aufmerksame Studium dieser sehr detaillierten historischen Analyse wird dringend empfohlen. Damit in engem Zusammenhang steht der unverantwortlich schlechte Wirkungsgrad der Dampfkraftwerke einschließlich der Atomkraftwerke, die den Dampfmaschinenprozeß einschließen. Hierzu wird vor allem auf STRACH (1991) verwiesen. Hierin heißt es u. a. (Zitat):

„Auch die Vorstellung, das ca. 80 °C heiße Kondensat, das als „Abfall“ aus der Dampfmaschine anfällt, für Fernwärme zu nutzen, ist so verlockend wie unrealistisch. – Die Produktionsprozesse, die rund um die Uhr laufen müssen, stellen 8600 Stunden im Jahr Fernwärme zur Verfügung. ‚Doch jeder Klempner weiß, daß in unseren Breitengraden durchschnittlich nur 1400 Stunden Wärme benötigt werden‘, berichtet Strach. Angebot und Nachfrage sind asynchron, und in kalten Wintertagen reicht dann auch die Fernwärme zur Deckung des Heizbedarfs nicht aus.“ (Ende des Zitats)

Besonders tragisch ist, daß durch das Dogma der Thermodynamik die wissenschaftliche Weiterentwicklung in sehr unerfreulicher Weise blockiert wird. Hierzu wird auf HILSCHER (1981) und BARTH (1987) hingewiesen. Bei BARTH (1987) heißt es ganz am Schluß (Zitat):

„Die mechanische Wärmetheorie mit ihren zahlreichen mathematischen und physikalischen Fehlern, mit Wärmetod und „Entropie“ versperrt jeden echten Fortschritt.“ (Ende des Zitats)

Literatur:

BARTH, G. (1962): „Rationale Physik“, Verlag „Wissen im Werden“, A-2063 Zwingendorf, Österreich, Haus Bradley

BARTH, G. (1975): „Energetische Wärmetheorie“, Verlag „Wissen im Werden“, A-2063 Zwingendorf, Österreich, Haus Bradley

BARTH, G. (1986): „Wenn Wärme nicht als „minderwertige“ Energie angesehen würde…“ aus Zeitschrift: „Sonnenenergie“ 5/86, S. 30 – 31

BARTH, G. (1987): „Die Fehler der mechanischen Wärmetheorie“, aus „raum & zeit“ 30/87, S. 78 – 82

BLÖSS, Chr. (1985): „Der Entropie-Begriff – Ein Irrtum und seine Folgen für die Thermodynamik“, DABEI-Colloquium Heft 3, Bonn

CARNOT, S. (1824): „Betrachtungen über die bewegende Kraft des Feuers“, Reihe Ostwalds Klassiker, Bd. 37, Leipzig 1909

CERBE / HOFFMANN (1982): „Einführung in die Wärmelehre“, 6. Auflg., Carl Hanser Verlag, München, Wien

CLAUSIUS, R. (1887): „Die mechanische Wärmetheorie“, Bd. 1, 3. Auflg., Verlag Friedr. Vieweg, Braunschweig

FRIEBE, E. (1987): „Wo liegen die ursächlichen Irrtümer in der theoretischen Thermodynamik?“, Zeitschr. „raum & zeit“, 28/87, S. 68 – 71

FRIEBE, E. (1988): „Die Widersprüche der Thermodynamik“, Zeitschr. „raum & zeit“, 36/88, S. 84 – 86

FRIEBE, E. (1990): „Das Energie-Erhaltungs-Prinzip – Ursache zahlreicher Mißverständnisse“, DPG-Didaktik-Tagungsband 1990, S. 654 – 659. Hrsg.: Prof. Dr. Wilfried KUHN, Gießen

HILSCHER, G. (1981): „Energie im Überfluß – Ergebnisse unkonventionellen Denkens“, Adolf Sponholtz Verlag, Hameln

HILSCHER, G. (1986): „Kohlendioxid als Arbeitsmittel nutzen – Ziel einer Neuentwicklung: Strom aus Solar- und Abwärme“, Zeitschr. „Sonnenenergie“ 3/86, S. 6 – 7

KIRCHHOFF, J. (1986): „Von der durchschaubaren Dampfmaschine zum nebulösen thermodynamischen Lehrinhalt“, Verlag Kirchhoff, Herten-Westerholt

KIRCHHOFF, J. (1987): „Zur Theorie und Praxis von Wärmekraftmaschinen“, Zeitschr. „Sonnenenergie“ 1/87, S. 12 – 15

KIRCHHOFF, J. (1990): „PERPETUUM MOBILE und Klima-Katastrophe“, aus „raum & zeit“ 45/90, S. 82 – 86, und 46/90, S. 72 – 82

STRACH, L. (1991): „Abwärme bringt Heißluft-Turbine auf Touren“, Zeitungsbericht von B. B. aus „VDI Nachrich

•  Homepage