Blog Ekkehard Friebe

FRIEBE, Ekkehard (1987): „Irrtümer in der Elektronentheorie?“,
Zeitschr. „raum & zeit“, 30/87, S. 82 – 85
________________________________________________________________

In der Ausgabe Nr. 28 von „raum & zeit“ hat der Autor bereits zu den Irrtümern in der theoretischen Thermodynamik Stellung genommen. Heute beschäftigt sich Ekkehard Friebe mit der orthodoxen Elektronentheorie und insbesondere mit der Deutung einer „Geschwindigkeitsabhängigkeit der Masse“, die er als kostspieligsten Irrtum der Physikgeschichte bezeichnet.

Die Grundannahmen der Elektronentheorie

In seinem Buch: „Das Relativitätsprinzip“ schreibt LAUE (Zitat aus LAUE 1911, 5. 27/ 28):

„Die Elektronentheorie ist das Ergebnis der folgenden drei Gedanken:
1. Die Elektrizität ist atomistisch konstituiert.
2. Elektromagnetische Felder werden nur von Elektronen erregt und wirken nur auf Elektronen; sie haben ausschließlich im Äther ihren Sitz. Die ponderablen Körper kommen nur in zweiter Linie in Betracht, insofern sie Elektronen enthalten.
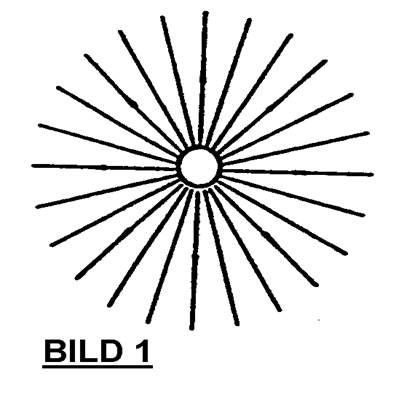
3. Der Äther ist ein alles durchdringender, starrer Körper und definiert so ein bestimmtes System, auf welches die Feldgleichungen zu beziehen sind. – Die Feldgleichungen selbst gehen aus den MAXWELLschen hervor, wenn . . . . . .“ (Ende des Zitats). Weiter führt LAUE (1911, S.28 und 95) aus: „Die Elektronen werden in manchen Teilen der Theorie als starre Kugeln gedacht, doch ist in vielen anderen Teilen keine Annahme über ihre Gestalt nötig Das Kraftfeld einer ruhenden Kugel mit gleichförmiger Oberflächenladung ist der Gleichwertigkeit aller Richtungen wegen durch eine Reihe radialer Kraftlinien mit konstantem Winkelabstand bestimmt. Die Potentialflächen sind Kugeln, deren Radien wie die reziproken Werte der abnehmenden Reihe der ganzen Zahlen wachsen, wenn man das Potential stets um den gleichen Betrag verkleinert, denn . . . . . . .“ (Ende des Zitats; vgl. auch BILD 1 bis 3.).

Elektrostatik

Die klassische Elektrostatik geht von einem Ansatz aus, der eine elektrisch geladene Kugel voraussetzt, die von einer gegenpolig geladenen Kugelschale mit unendlich großem Radius kugelsymmetrisch umgeben ist. Daraus resultieren kugelsymmetrische Verhältnisse für die Kraftlinien (Feldlinien) des elektrostatischen Feldes (BILD 1).

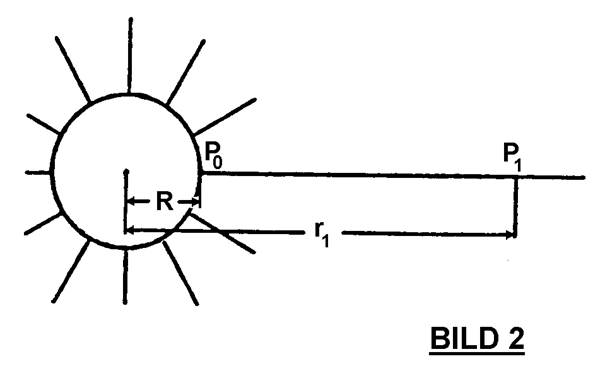
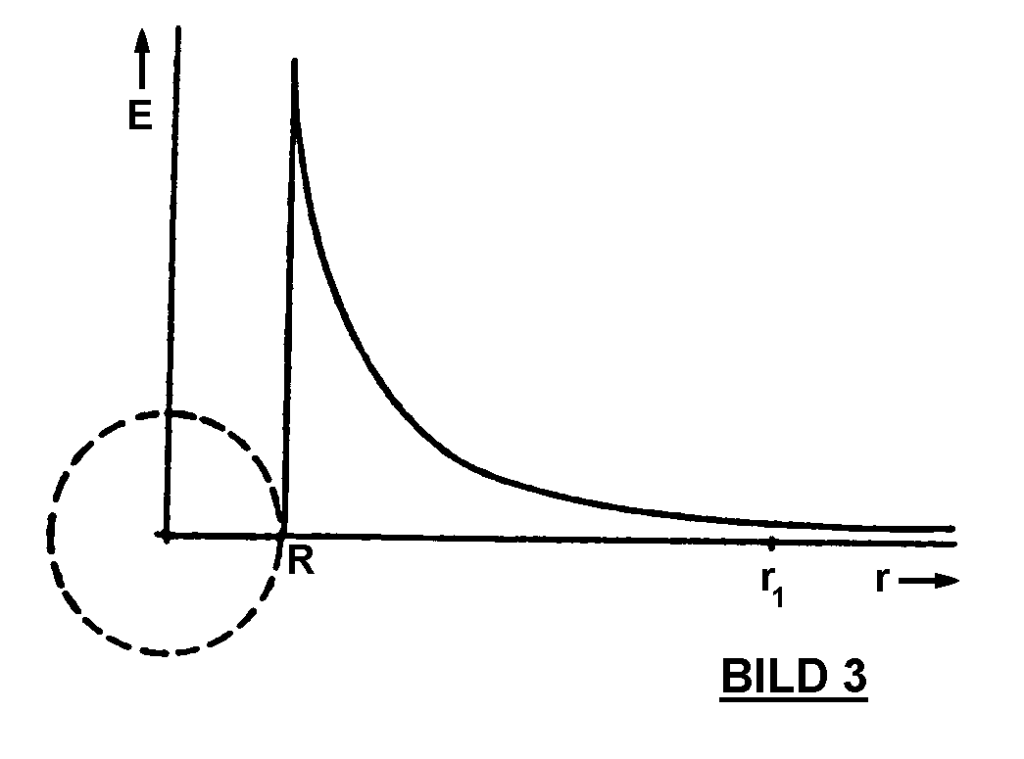
Die Kugelsymmetrie an sich sagt noch nichts über die räumliche Abhängigkeit der Feldstärke (Kraft-Intensität am Ort der Kraftlinien) aus. Deshalb hat man rein axiomatisch festgelegt, daß die Feldstärke im Feld-raum eine quadratische Abhängigkeit vorn Kehrwert der Entfernung vom Mittelpunkt der inneren Kugel besitzen solle (BILD 2 und 3). Diese Darstellung ist zwar eine sich aus der Kugelsymmetrie anbietende Möglichkeit, sie folgt aber keineswegs zwingend. Deshalb wird in einzelnen Lehrbüchern behauptet, daß diese Zuordnung durch Meßergebnisse, die dem „COULOMBschen Gesetz“ zugrunde liegen, experimentell bestätigt sei. Diese Aussage bedarf einer näheren Untersuchung:

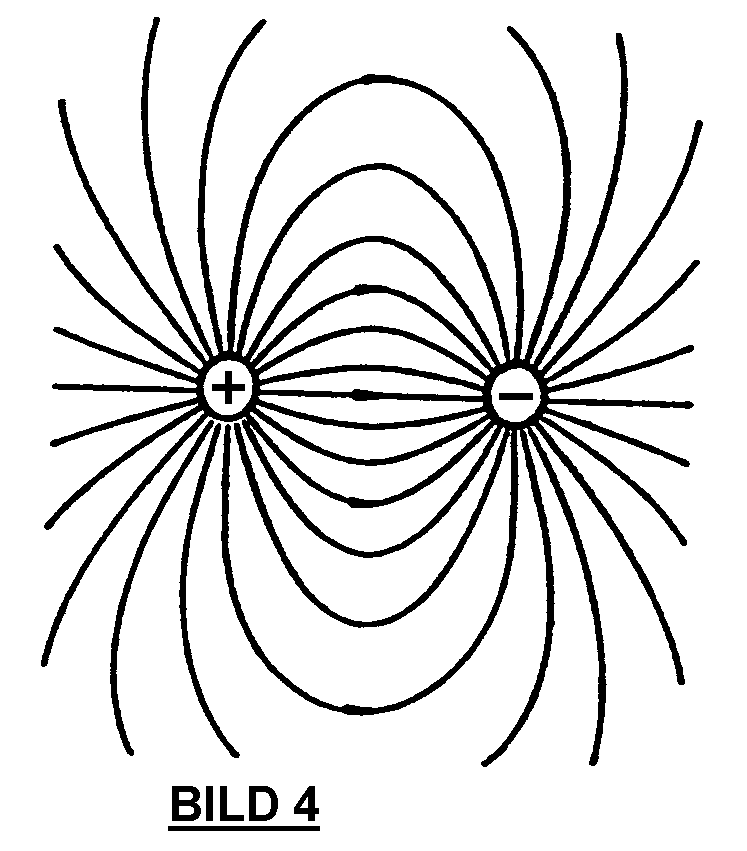
Das „COULOMBsche Gesetz“ geht aus von zwei gleich großen, gegenpoligen, felderzeugenden Kugel-Ladungen, zwischen denen eine Wechselwirkung (actio = reactio) gegeben ist (BILD 4). Dabei ist das Kraftfeld räumlich begrenzt, denn die Kraftlinien sind gekrümmt und beginnen an der einen und enden an der anderen Kugel-Ladung. Die Zuordnung beim radialsymmetrischen Feld gemäß BILD 1 dagegen setzt eine einzige felderzeugende Kugel-Ladung voraus, deren Kraftlinien linear sind, sich aber bis ins Unendliche erstrecken. Das „COULOMBsche Gesetz“ kann daher als experimentelle Grundlage für die angeblich quadratische Abhängigkeit nicht herangezogen werden.

Die axiomatisch vorgegebene quadratische Abhängigkeit führt rein rechnerisch zu einer endlichen Kapazität einer (metallischen) Kugel, die sich vollkommen allein im weiten Kosmos befindet. Dies ist absolut unrealistisch. Denn es ist unmöglich, eine Kapazität lediglich einpolig zu messen. Eine elektrische Kapazität läßt sich deshalb sinnvoll nur definieren alsWechselwirkung zwischen zwei leitenden Oberflächen. Andernfalls ist das Prinzip actio = reactio verletzt. Zu der Wichtigkeit dieses Prinzips wurde schon in anderem Zusammenhang ausführlich Stellung genommen (SCHMIDT 1985, FRIEBE 1985).

Die rein rechnerische Endlichkeit der Kapazität einer Kugel im unendlichen Kosmos ist aus den dargelegten Gründen ein starkes Indiz gegen die postulierte quadratische Abhängigkeit.

Die eigentlichen Schwierigkeiten des radialsymmetrischen Ansatzes ergeben sich aber erst, wenn man die felderzeugende Kugel-Ladung zusammen mit einer zweiten Ladung betrachten will. Hierzu gibt es zwei Möglichkeiten: a) Die zweite Ladung wird selbst als feldfrei angesehen, so daß sie das ursprüngliche Feld nicht verändert. b) Die Felder beider Ladungen werden vektoriell überlagert (Superposition).

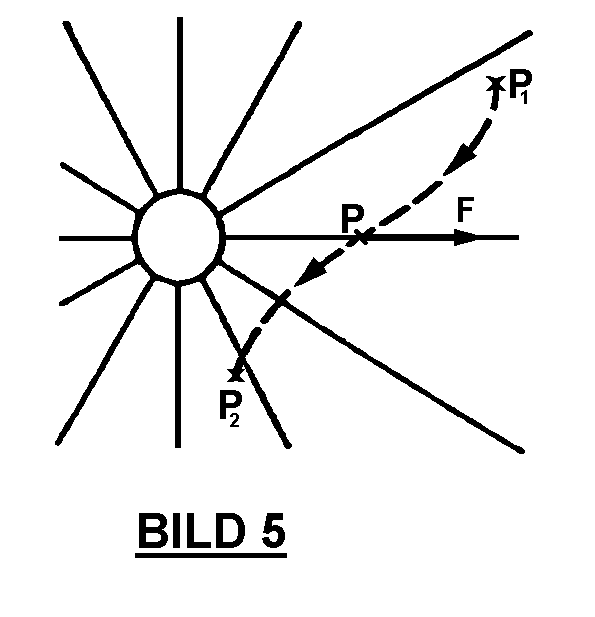
Obwohl die Möglichkeit b) die exaktere ist, da sie gleichartige Ladungen auch gleichartig behandelt, hat sich die Theoretische Physik dennoch für die Darstellungsart a) entschieden, da sie mathematisch einfacher ist. Hierbei wird unausgesprochen eine Unterscheidung vorgenommen zwischen einer aktiven, felderzeugenden Ladung und einer passiven Ladung. Es wird also – rein willkürlich – bei einer Ladung das „Eigenfeld“ vernachlässigt (BILD 5). In dem durch eine aktive Ladung erzeugten kugelsymmetrischen Feld wird für jeden Aufpunkt P an dem sich eine (passive) Ladung befindet, eine Kraft F definiert, die in Richtung der radialen Feldlinien liegt. Die tatsächlich auftretende betragsmäßige Feldänderung und Feldverzerrung wird unberücksichtigt gelassen.

Es wird die Formel für die sogenannte elektrostatische „LORENTZ-Kraft“ als Definitions-Gleichung verwendet [Glg. (1)]:

F = e · E

mit: F = Kraft zwischen aktiver und passiver Ladung,
e = Elementar-Ladung des passiven Elektrons,
E = elektrische Feldstärke der aktiven Ladung,
wobei Vektoren durch Fettdruck gekennzeichnet sind.

Um den durch die Vernachlässigung des „Eigenfeldes“ bedingten Fehler klein zu halten, hatte man im Rahmen der klassischen Elektrostatik zusätzlich die einschränkende Bedingung eingeführt. daß die aktive Ladung wesentlich größer sein sollte als die passive Ladung. Später hat man diese Bedingung bei der Elektronentheorie ganz aus den Augen verloren. obwohl gerade die „Elektronen“ definitionsgemäß sehr klein sind. Die Folge sind erhebliche numerische Fehler und vor allem qualitative Fehldeutungen.

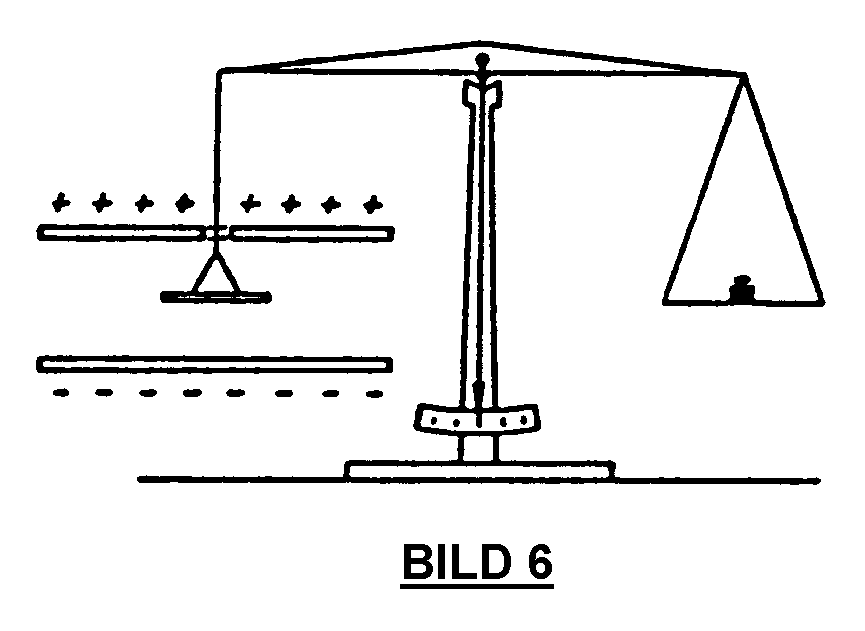
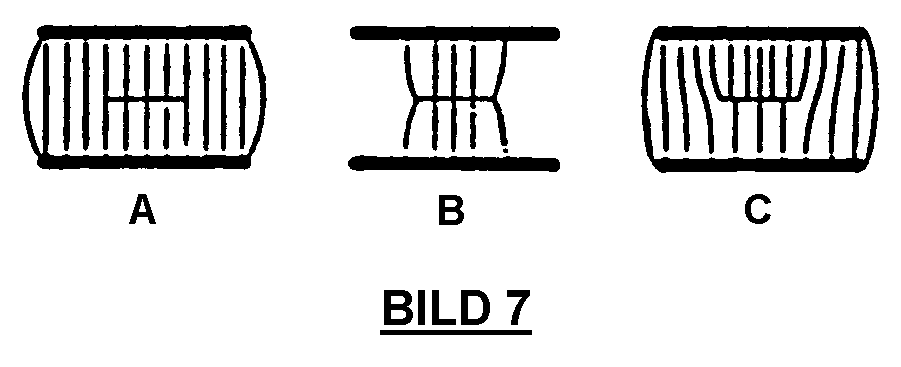
Besonders schwerwiegend ist nun eine Fehldeutung, die sich im Zusammenhang mit der Versuchsanordnung nach BILD 6 veranschaulichen läßt. Zwischen den beiden Platten eines Plattenkondensators ist eine kleinere, frei bewegliche dritte Platte aufgehängt, an der die elektrostatische Kraftwirkung gemessen werden kann. BILD 7 zeigt den Feldlinienverlauf:

A: die äußeren Platten sind gegenpolig geladen, die mittlere Platte trägt keine Ladung
B: die äußeren Platten sind gleichpolig geladen. die mittlere Platte trägt eine gegenpolige Ladung
C: die mittlere und untere Platte sind gleichpolig geladen, die obere Platte trägt eine gegenpolige Ladung. Man erkennt aus BILD 7C, daß das „Eigenfeld“ der kleineren Platte nicht vernachlässigbar ist. 

Besonders deutlich wird dies, wenn man jetzt die kleinere Platte bei unveränderter Ladung aus dem Feldraum der beiden großen Platten herausnimmt. Aufgrund ihres „Eigenfeldes“ wird die kleinere Platte weiterhin mit der oberen Platte in Wechselwirkung stehen, also eine elektrostatische Kraft in Richtung zur oberen Platte hin erfahren. Dagegen ergibt sich aus Glg. (1) eine Kraft gleich Null, da hier die Feldstärke der felderzeugenden großen Platten gleich NULL vorausgesetzt ist.

Der rechnerische Fehler wird noch größer, wenn die kleinere Platte in ein anderes, potential-getrenntes Feld, z. B. eines zweiten Plattenkondensators, gebracht wird. Hier errechnet sich gemäß Glg. (1) eine Kraft, die im wesentlichen von dem Feld zwischen den Platten des zweiten Kondensators bestimmt ist, obwohl – wegen der Potentialtrennung – die Ladung der kleineren Platte mit diesem Feld gar nicht in Wechselbeziehung steht.

Erst wenn beide Kondensatoren potentialmäßig verbunden werden, kann durch Influenzwirkung auch der zweite Kondensator mit der Ladung der kleineren Platte in Wechselwirkung treten. Die erforderliche Umladung benötigt jedoch eine endliche Zeit. Aus diesem Grunde können Hochenergiebeschleuniger, die im Prinzip aus einer sehr langen Kette von Einzel-Kondensatoren bestehen, eine Energiefortpflanzung nur in endlicher Zeit bewirken. Daher resultiert die sogenannte „Grenzgeschwindigkeit“.

Die Deutung einer „Geschwindigkeitsabhängigkeit der Masse“ ist offensichtlich falsch und wohl der kostspieligste Irrtum, der je in der Physikgeschichte gemacht wurde (vgl. FRIEBE 1983).

Durch die Vernachlässigung des „Eigenfeldes“ der einen beteiligten Ladung wird also der eingangs aufgestellte Grundgedanke verletzt, demgemäß nur eine Art von Elementar-Ladungen eingeführt werden sollte. Dennoch weist kein Lehrbuch auf die Unterscheidung von aktiver und passiver Ladung hin, denn es gibt im Rahmen der Elektronentheorie nur ein einziges Formelsymbol für das Elektron. Auch findet man nirgends eine Aussage, auf welche Art von Ladung sich die angeblichen experimentellen Bestätigungen zur realen Existenz des Elektrons beziehen.

Elektrodynamik

Im Rahmen der Elektrodynamik nimmt die Elektronentheorie an, daß ein bewegtes Elektron magnetische Wirkungen hervorruft. Hierzu wird das Produkt

Ladung mal Ladungsgeschwindigkeit

einem elektrischen Strom gleichgesetzt. Obwohl diese Annahme zunächst plausibel und nicht im Widerspruch zu experimentellen Befunden zu sein scheint, ist sie dennoch ohne klare Definition. Denn nach Fortfall der Ätherhypothese ist diese Annahme gleichbedeutend mit einer Festsetzung der Elektronen-Geschwindigkeit relativ zum Unendlichen. Eine derartige Definition ist aber unendlich vieldeutig und daher einer experimentellen Überprüfung und einer exakten mathematischen Behandlung nicht zugänglich. Die daraus resultierenden begrifflichen Schwierigkeiten sind die Ursache der zahlreichen Paradoxa der speziellen Relativitätstheorie (vgl. THEIMER 1977, 1986; GUT 1981).

Beseitigung der Schwierigkeiten

Die aufgezeigten Schwierigkeiten sind dadurch bedingt, daß nur eine Art von Ladungsträgern (negative Elementarladungen = Elektronen) vorausgesetzt ist. Die Schwierigkeiten lösen sich in erstaunlich einfacher Weise auf, wenn man auch positive Elementarladungen (Positronen) als gegeben annimmt, deren Eigenfeld voll berücksichtigt wird. Man erhält dann durch Überlagerung die bekannten Feldlinienbilder, die FARADAY schon 1836 nachgewiesen hat (BILD 4).

Die Positronen wurden bereits im Jahre 1932 durch ANDERSON in der WILSONschen Nebelkammer entdeckt. Dennoch wurde diese Entdeckung bis heute noch nicht in konsequenter Weise weiterverfolgt. Durch Einführung der Positronen (anstelle von „Löchern“ oder „passiven Ladungen“) unter Verwendung der in der Technik allgemein üblichen Strom-Definition:

Ladung pro Zeiteinheit

bezogen auf einen Bezugsquerschnitt werden alle elektro-magnetischen Erscheinungen auf reine Wechselwirkungen zurückführbar. Der Begriff des Unendlichen verschwindet. Das Relativitätsprinzip in seiner klassischen Form, wie es EINSTEIN ursprünglich gefordert hatte, sowie das Prinzip „actio = reactio“, das dem qualitativen Befund der Experimente zum „COULOMBschen Gesetz“ entspricht, werden widerspruchsfrei anwendbar.

Es würde zu weit führen, hierauf an dieser Stelle im einzelnen einzugehen. Es wird auf die Arbeit: „Analyse des physikalischen Aussagegehalts der MAXWELLschen Elektrodynamik“ (FRIEBE 1985) verwiesen, wo eine entsprechende Modellvorstellung entwickelt wird.

Anregungen für den Physik-Unterricht

a) Der Begriff der Kapazität einer Kugel im unendlichen Feldraum sollte gestrichen werden. Die Kapazität ist ausschließlich am Platten-Kondensator einzuführen und klar als Wechselwirkung zwischen zwei leitenden Oberflächen zu definieren.

b) Es ist im Unterricht stets darauf hinzuweisen, daß die Formel für die „LORENTZ-Kraft“ nur eine Näherung darstellt, die kleine passive Ladungen und Potentialbindung zwischen verschiedenen Feldern und langsame Vorgänge zur Voraussetzung hat.

c) Der Begriff der „Geschwindigkeitsabhängigkeit der Masse“ sollte als historisch interessante Folgerung aus ungeeigneten Prämissen dargestellt werden.

LITERATUR

EINSTEIN, A. (1905): Zur Elektrodynamik bewegter Körper. „Annalen der Physik“, Bd. 17, S. 891 – 921

EULER, K.-J. (1981): Eine Entdeckung verändert die Welt. Sonderheft der Zeitschrift: „elektrotechnik“, S. 10 – 15

FRIEBE, E. (1983): Gibt es einen experimentellen Beweis für die sog. „Geschwindigkeitsabhängigkeit der Masse“? DPG-Tagung, Gießen

FRIEBE, E. (1984): Kritische Betrachtungen zur klassischen Elektro-Statik. Zeitschr. „Wissen im Werden“, Zwingendorf, 1984, H.2, S.3-7

FRIEBE, E. (1985): Analyse des physikalischen Aussagegehalts der MAXWELLschen Elektrodynamik. DABEI-Colloquium, Bonn, 1985, H.2

GUT B. J. (1981): Immanent-logische Kritik der Relativitätstheorie. Verlag Rolf Kugler, CH 6317 Oberwil b. Zug

HUND, F (1980): Wer hat die Relativitätstheorie geschaffen? Phys. B1., Bd. 36, H.8, S.237-240, Physik Verlag GmbH, Weinheim

JAMMER, M. (1964): Der Begriff der Masse in der Physik. Wissenschaftliche Buchgesellschaft, Darmstadt

KÜPFMÜLLER, K. (1973): Einführung in die theoretische Elektrotechnik. 10. Auflg., Springer, Berlin, Heidelberg, New York

LAUE, M. (1911): Das Relativitätsprinzip. Friedr. Vieweg, Braunschweig

LORENTZ, H. A. (1885): Versuch einer Theorie der elektrischen und optischen Erscheinungen in bewegten Körpern. Leiden 1985

MESCHKOWSKI, H. (1976): Richtigkeit und Wahrheit in der Mathematik. Bibliographisches Institut Mannheim, Wien, Zürich

POHL, R. W.(1960): Elektrizitätslehre. Springer, Berlin, Göttingen, Heidelberg, 17. Auflg.

POPPER, K.(1982): Logik der Forschung. Verlag Mohr, Tübingen, 7. Auflg.

SCHMIDT, W. (1985): Irreversible Wechselwirkungen und deren Anwendung. DABEI-Colloquium, Bonn, 1985, H.1

THEIMER, W.(1977): Die Relativitätstheorie. Lehre – Wirkung – Kritik. Francke, Bern und München

THEIMER, W.(1986): Handbuch naturwissenschaftlicher Grundbegriffe. Francke, Tübingen

ZIMAN, J.(1982): Wie zuverlässig ist wissenschaftliche Erkenntnis? Friedr. Vieweg, Wiesbaden. Reihe: Facetten der Physik

• Homepage