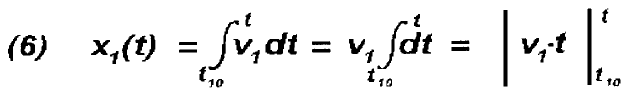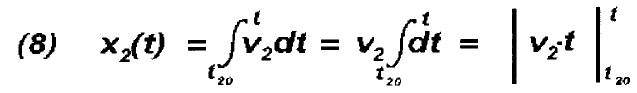Integrations- Konstanten

XVIII. Integrations-Konstanten

FRIEBE, E. (1985): „Die Bedeutung der Integrations-Konstanten für die mathematische Beschreibung von Bewegungsvorgängen“, DPG-Didaktik-Tagungsband 1985, S. 557 - 562. Hrsg.: Prof. Dr. Wilfried Kuhn, Gießen

Die Bedeutung der Integrations-Konstanten für die mathematische Beschreibung von Bewegungsvorgängen

Ekkehard FRIEBE, München (Überarbeitete Fassung)

Alltäglich begegnen uns Bewegungsvorgänge: Die Bewegung eines Fahrzeuges, Schiffes oder Flugzeuges, die Flugbahn eines Geschosses und vieles andere. Man sollte meinen, daß zur mathematischen Beschreibung von Bewegungsvorgängen eine zweifelsfreie Methode allgemein bekannt ist und angewandt wird. Dies ist aber nicht der Fall.

1. Linear-gleichförmige Bewegungsvorgänge

Betrachten wir zunächst einen linear-gleichförmigen Bewegungsvorgang in einem kartesischen Koordinaten-System. Für die Beschreibung eines solchen Vorgangs ist nur eine räumliche Koordinaten-Achse x ausreichend. Diese Darstellung hat den Vorteil, daß man die Raum-Koordinate zusammen mit der Zeit-Koordinate in einer Ebene - z.B. auf dem Zeichnungspapier - auftragen kann. Denn mehrdimensionale Raum-Zeit-Probleme bereiten erfahrungsgemäß in der Veranschaulichung Schwierigkeiten. Und gerade die Veranschaulichung ist ein wesentliches Hilfsmittel, um Probleme der analytischen Mathematik verständlich zu machen und um Irrtümer möglichst frühzeitig zu erkennen.

Bild 1 zeigt einen solchen linear-gleichförmigen Bewegungsvorgang v₁. Dabei ist als Abszisse die Zeit t und als Ordinate der Ort x aufgetragen. Die Gerade, die den Bewegungsvorgang im Koordinaten-System S_A darstellt, geht durch den Koordinaten-Ursprung, d.h. durch den Schnittpunkt beider Koordinaten-Achsen. Diese Zuordnung ist mitunter zweckmäßig, weil hierbei die Geschwindigkeit durch den folgenden einfachen Ausdruck beschrieben werden kann:

(1) v₁ = x₁(t) / t

(hierbei ist gesetzt: Geschwindigkeit = Orts-Koordinate / Zeit-Koordinate)

Diese Darstellung setzt voraus, daß der Nullpunkt der Zeitrechnung so festgelegt ist, daß er mit dem Beginn des Bewegungsvorgangs zusammenfällt. Dies ist eine Festlegung, wie sie im Sport allgemein üblich ist, indem man die Stoppuhr mit dem Beginn eines Wettlaufs in Bewegung setzt.


2. Zeitlich gegeneinander versetzte Bewegungsvorgänge

Ist nun diese einfache Darstellung mit Nullsetzen des Zeitablaufs stets zulässig? Diese Frage muß verneint werden. Denn sobald mehrere linear-gleichförmige Bewegungsvorgänge beschrieben werden sollen, die nicht gleichzeitig beginnen, kann die Geschwindigkeit - auch bei linearen Vorgängen - mathematisch allgemeingültig nur beschrieben werden [siehe Glg. (2)] durch den

Differential-Quotienten (Geschwindigkeit = Wegdifferential / Zeitdifferential).

Betrachten wir zunächst zwei linear-gleichförmige Bewegungsvorgänge, die jeweils eine konstante Geschwindigkeit v₁ bzw. v₂ haben. Man erhält als Differential-Quotient (Bild 2 ):

(2) v₁ = dx₁(t) / dt v₂ = dx₂(t) / dt (3) dx₁(t) = v₁ dt dx₂(t) = v₂ dt

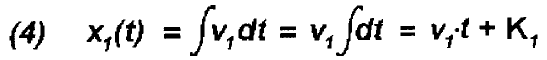
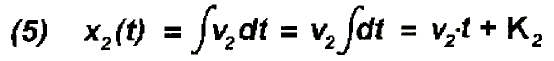
x₁(t) bzw. x₂(t) ist die analytische Beschreibung des jeweiligen Bewegungsvorgangs, wobei K₁ und K₂ vieldeutige Integrations-Konstanten sind, die nur durch Festlegung der Integrations-Grenzen ermittelt werden können. Ohne diese Festlegung spricht man von einem „unbestimmten Integral“.

Zur Bestimmung der Integrations-Konstanten betrachten wir Bild 2 und denken beispielsweise an einen sportlichen Wettlauf, bei dem zum Zeitpunkt t_ü ein Überholvorgang stattfindet. Der Soll-Startpunkt (Startschuß) liege bei t = 0 (Festsetzung). Die beiden tatsächlichen Start-Zeitpunkte werden mit t₁₀ und t₂₀ angenommen. Wir erhalten als analytische Beschreibung (bestimmtes Integral):

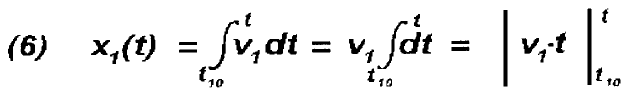
(7) x₁(t) = v₁·t - v₁·t₁₀
und in analoger Weise:

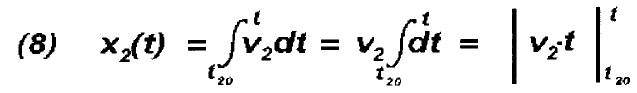
(9) x₂(t) = v₂·t - v₂·t₂₀
Dabei entsprechen v₁·t₁₀ = K₁ und v₂·t₂₀ = K₂ den oben eingeführten Integrations-Konstanten. Bei diesen Integrationen ist die obere Integrations-Grenze - und nur diese - variabel.

Die vorstehende Methode zur Bestimmung der Integrations-Konstanten wird in zahlreichen Lehrbüchern richtig dargestellt. Es erübrigt sich deshalb, hier eine weitere Erläuterung. Sie gilt anerkanntermaßen für alle klassischen Bewegungsvorgänge ganz unabhängig davon, ob ein Wettlauf, ein ballistisches Problem (Gewehr-Geschoß), ein Schallausbreitungs-Problem (Medium Luft in Verbindung mit bewegtem Sender und Empfänger) o.ä. betrachtet wird. Dennoch werden die Integrations-Konstanten bei der Behandlung von Problemen mit mehr als einem Koordinaten-System oftmals irrtümlich außer acht gelassen.
3. Mehr als ein Koordinaten-System

Betrachten wir zunächst zwei relativ zueinander ruhende Koordinaten-Systeme S_A und S_B mit dem festen Abstand a_AB gemäß Bild 3. Hierbei ergeben sich bereits bei einem Bewegungsvorgang ähnliche Überlegungen wie im vorhergehenden Abschnitt. Der Bewegungsvorgang mit der konstanten Geschwindigkeit v₁ durchlaufe die Abszissenachse des Systems S_A im Zeitpunkt t_10A. Dann durchläuft er die Abszissenachse des Systems S_B zu einem Zeitpunkt t_10B, der notwendigerweise von t_10A verschieden ist. Der Bewegungsvorgang ist in beiden Systemen wie folgt zu beschreiben:

(10) x_1A(t) = v₁·t - v₁·t_10A = v₁·t - K_A

(11) x_1B(t) = v₁·t - v₁·t_10B = v₁·t - K_B

Obwohl also in beiden Systemen nur eine konstante Geschwindigkeit v₁vorausgesetzt ist, sind dennoch die Integrations-Konstanten K_A bzw. K_B der beiden Fälle verschieden. Deshalb ist die Geschwindigkeits-Definition gemäß Bild 1 und GIg. (1) unzulässig. Es ist allerdings möglich, durch Wahl des Zeitbeginns, z.B. durch Festsetzung von t_10A = 0, eine (aber nur eine) Integrations-Konstante zu NULL zu machen.

4. Zwei Koordinaten-Systeme relativ zueinander bewegt

Nun ist der Übergang auf zwei relativ zueinander bewegte Koordinaten-Systeme nicht mehr schwer. Der Abstand a_AB beider Systeme ist nicht mehr konstant, sondern durchläuft zeitlich nacheinander größer werdende oder kleiner werdende Abstandswerte. Die sogenannte „Integrations Konstante“ wird jetzt - im Gegensatz zu den bisherigen Betrachtungen - eine lineare Funktion der Zeit. Man könnte von einer „gleitenden lntegrations-Konstante“ sprechen. Die Ursache der Zeitabhängigkeit liegt darin, daß der Koordinaten-Ursprung selbst einem Bewegungsvorgang unterliegt. Hierdurch wird auch die untere Integrations-Grenze variabel.

Die Auswertung ergibt, worauf hier nicht im einzelnen eingegangen werden soll, daß ein Bewegungsvorgang, der im System S_A die Geschwindigkeit v₁ hat, im System S_B, das relativ zu S_A mit der Geschwindigkeit w bewegt ist, die Geschwindigkeit v₁ + w bzw. v₁ - w besitzt. Es gilt also die klassische Addition der Geschwindigkeiten. Dies überrascht nicht, da bisher ausschließlich klassische Bewegungsvorgänge betrachtet wurden.

5. Ausblick auf Lichtausbreitungs-Vorgänge und Relativitäts-Theorie

Auch Lichtausbreitungs-Vorgänge unterliegen - entgegen einer weitverbreiteten Meinung - denselben mathematischen Beschreibungs-Gesetzen, da man eine Konstanz der Ausbreitungs-Geschwindigkeit als Annahme voraussetzt. Auch hierbei sind die Integrations-Konstanten wesentlich. Bei der Relativitäts-Theorie wurde irrtümlich - ausgehend vom einfachsten Fall gemäß Bild 1, bei dem sich die Integrations-Konstante zu NULL ergibt, - dieser Wert NULL auch für mehrere Bezugs-Systeme als richtig unterstellt, obwohl hierbei höchstens eine Integrations-Konstante gleich NULL gesetzt werden darf .

So ergibt sich aus dem fälschlich verwendeten Ansatz
(mit c = Lichtgeschwindigkeit und v = relative System-Geschwindigkeit):

(12) c = x/t und v = x/t
(hier wurden irrtümlich Quotienten statt Differential-Quotienten verwendet)

die Zuordnung: (13) c = v .
(vergleiche dazu die Arbeit von Walter DISSLER (1971): „Führt der Glaube an Einsteins Relativitätstheorie zu einer gewissen Art geistiger Invalidität?“)

Dadurch wird die LORENTZ-Transformation wertlos. Denn mit c = v ergibt sich der LORENTZ-Faktor zu:
gamma = [1 - (v/c)²]^-1/2 = unendlich.

Auch das „relativistische Additions-Theorem der Geschwindigkeiten“ mit den drei Geschwindigkeiten c, v und w beruht auf der impliziten Prämisse:

(14) c = x/t; v = x/t; w = x/t.
(auch hier wurden irrtümlich Quotienten statt Differential-Quotienten verwendet)

und damit:

(15) c = v = w .

Deshalb hat auch dieses Theorem keine mathematisch auswertbare Grundlage.

Bei der Annahme der Konstanz der Lichtgeschwindigkeit muß - zur Bestimmung der „gleitenden lntegrations-Konstanten“ - unterschieden werden, relativ wozu diese Konstanz definiert werden soll: Relativ zur Lichtquelle, relativ zu einem gedachten Lichtmedium oder relativ zu einem sonstigen System. Denn der Geschwindigkeitsbegriff (Abstandsänderung pro Zeiteinheit) ist seinem Wesen nach stets eine relative Größe, da ein Abstand niemals einem einzelnen Punkt zugeordnet werden sondern nur zwischen (mindestens) zwei Punkten gedacht werden kann. Nach Bereinigung der aufgezeigten mathematischen Irrtümer gilt wieder - unter anderem - die klassische Addition der Geschwindigkeiten.

Die Behauptung, die Relativitäts-Theorie sei experimentell vielfach bestätigt, ist nicht stichhaltig. Denn infolge der Irrtümer ist diese Theorie in sich widersprüchlich und deshalb experimentell nicht bestätigbar. Denn jedes Experiment zu Gunsten der Theorie ist notwendigerweise - wegen der inneren Widersprüche - gleichzeitig ihre eigene Widerlegung.


Literatur:

BARTH, Gotthard: „Wurde die Welt betrogen?“, Zeitschr. „raum & zeit“ 1987, Heft 28, S. 64 - 68

BRINKMANN, Karl: „Zu Zeit und Raum - Gegen die Relativitätstheorie“, Verlag Johannes Berchmans, München, 1984

DISSLER, Walter: „Führt der Glaube an Einsteins Relativitätstheorie zu einer gewissen Art geistiger Invalidität?“, Zeitschrift: „Wissen im Werden“, Österreich 1971, H. 1, S. 62 - 69

FRIEBE, Ekkehard: „Wie es zur Relativitätstheorie kam“, Zeitschr. „raum & zeit“ 1988, Heft 34, S. 86 - 89

GUT, Bernardo: „Immanent-logische Kritik der Relativitätstheorie“, Verlag Rolf Kugler, CH 6317 Oberwil b. Zug, 1981

KRETSCHMAR, Harry: „Neue Betrachtungen zur Relativitätstheorie“, Zeitschr. „raum & zeit“ 1987, Heft 26, S. 46 - 52

KUHN, Wilfried: „Das Wechselspiel von Theorie und Experiment im physikalischen Erkenntnisprozeß“, DPG-Didaktik-Tagungsband 1983, S. 416 - 438.

MURRAY, W. A. SCOTT: „The roots of relativity“, Zeitschr. „Wireless World“, May 1984, S. 69 - 72

NEUBER, Heinz: „Technische Mechanik“, Dritter Teil: „Kinetik“, Verlag Springer, Berlin/Heidelberg/New York, 1974, insb. Abschnitte: 2.6 bis 2.11, S. 10 - 24

PAGELS, Kurt: „Mathematische Kritik der spez. Relativitätstheorie“, Verlag Rolf Kugler, CH 6317 Oberwil b. Zug, 1985

SCHMIDT, Wolfgang: „Quellen des Nichtwissen“, Vier Vorträge vor der Deutschen Physikalischen Gesellschaft, 1981

THEIMER, Walter: „Die Relativitätstheorie - Lehre, Wirkung, Kritik“, Verlag Francke, Bern / München, 1977

WEHR, Günther: „Neue Relativitätstheorie“, Verlag Peter D. Lang, Frankfurt-M./Bern/Cirencester, U. K., 1980

Homepage